
Photo by Edi Kurniawan on Unsplash
Predicting the Likelihood of E-signing a Loan Based on Financial History
1. Introduction
In the financial lending industry, companies evaluate applicants by analyzing their financial backgrounds to determine risk levels and make informed decisions on loan approvals and terms. While companies can rely on direct applicants via websites or mobile apps, many also partner with Peer-to-Peer (P2P) lending marketplaces to expand their reach. P2P marketplaces, like LendingTree, Upstart, and LendingClub, serve as intermediaries, connecting applicants to lenders and offering options based on applicants’ financial details.
In this project, we focus on a specific part of the lending process: identifying which applicants are likely to complete the electronic signature (e-sign) step in the onboarding funnel. Completing the e-sign step indicates strong interest, signaling that the applicant is a quality lead worth further engagement. By predicting e-sign completion rates, we can help lending companies optimize their onboarding experience, ultimately increasing the likelihood of applicants moving forward with a loan offer.
Our goal is to build a predictive model to assess the quality of leads acquired through P2P marketplaces by forecasting the likelihood of reaching this e-sign step. Such a model empowers lenders to tailor their processes, engage high-quality applicants, and reduce drop-off rates. This model also underscores how companies can leverage data-driven decisions to enhance their operational efficiency and better allocate resources to high-potential leads.
2. Understanding the Data
To build an effective model for predicting e-sign completion, it’s essential to understand the dataset that serves as the foundation of our analysis. The data used in this project comes from P2P lending marketplaces, which provide a wealth of information about loan applicants even before they enter the lender’s onboarding process. This data includes not only personal details but also financial metrics designed to help assess applicant quality.
Data Sources and Key Features
The dataset includes several categories of information, giving a comprehensive view of each applicant’s financial background:
Demographic Information: Basic details such as age and years employed provide insight into the applicant’s background and financial stability.
Income and Employment History: Features like monthly income and the number of years employed help gauge the applicant’s earning potential and job stability.
Risk and Quality Scores: The dataset includes a set of risk scores created by the lender’s internal teams based on applicants’ financial histories. These risk scores indicate the likelihood that an applicant will meet loan requirements or adhere to the onboarding process. Additionally, the P2P marketplaces provide their own quality scores, which offer an external assessment of each lead.
Additional Financial Indicators: Data on debt, homeownership, account age, and credit inquiries in the past month give further context for each applicant’s financial status and potential reliability.
Response Variable
The key response variable in this dataset is e_signed, a binary variable indicating whether or not an applicant completed the e-sign step in the loan application process. If an applicant reaches this final screen, they are considered a quality lead, likely to follow through with the loan application. Thus, the goal of our model is to predict the likelihood of an applicant reaching this step, based on the other variables in the dataset.
Data Characteristics
Given the dataset’s breadth, we’ll examine how each feature contributes to predicting e-sign completion in later sections. The dataset also includes categorical variables, like pay_schedule, that indicate the frequency of an applicant’s income (weekly, biweekly, etc.), as well as several numerical features with varying ranges and distributions. Each feature provides valuable context for building a model that accurately forecasts e-sign completion rates.
With this understanding of the data, we’re now ready to move into exploratory data analysis (EDA), where we’ll explore patterns, relationships, and distributions that could impact model performance.
3. Exploratory Data Analysis (EDA)
Exploratory Data Analysis (EDA) is a crucial step to better understand the patterns and relationships within our data, allowing us to make informed decisions during model development. In this section, we’ll load the data, check for any missing values, visualize feature distributions through histograms, and examine feature correlations with the target variable, e_signed. These steps ensure we have a solid understanding of the dataset’s structure before moving to feature engineering and model training.
Data Housekeeping
The first step in EDA is to load the data and perform basic checks to understand its structure:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sn
# Loading the dataset
dataset = pd.read_csv('financial_data.csv')
dataset.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 17908 entries, 0 to 17907
Data columns (total 21 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 entry_id 17908 non-null int64
1 age 17908 non-null int64
2 pay_schedule 17908 non-null object
3 home_owner 17908 non-null int64
4 income 17908 non-null int64
5 months_employed 17908 non-null int64
6 years_employed 17908 non-null int64
7 current_address_year 17908 non-null int64
8 personal_account_m 17908 non-null int64
9 personal_account_y 17908 non-null int64
10 has_debt 17908 non-null int64
11 amount_requested 17908 non-null int64
12 risk_score 17908 non-null int64
13 risk_score_2 17908 non-null float64
14 risk_score_3 17908 non-null float64
15 risk_score_4 17908 non-null float64
16 risk_score_5 17908 non-null float64
17 ext_quality_score 17908 non-null float64
18 ext_quality_score_2 17908 non-null float64
19 inquiries_last_month 17908 non-null int64
20 e_signed 17908 non-null int64
dtypes: float64(6), int64(14), object(1)
memory usage: 2.9+ MB
The dataset contains 17,908 entries with 21 columns. Key details include:
ID and Demographic Information: Columns like
entry_id,age,pay_schedule, andhome_owner.Financial Data: Includes income, employment duration (in months and years),
current_address_year,personal_account(in months and years), andhas_debt.Loan Information: Covers
amount_requested, fiverisk_scorefields, and two external quality scores.Credit Activity:
inquiries_last_monthtracks recent credit inquiries.Target Variable:
e_signed, which indicates if the applicant completed the e-sign step.
All columns are fully populated, with data types including integers, floats, and one object (for pay_schedule). Total memory usage is around 2.9 MB.
After loading, we inspect the initial rows of the dataset and check for any missing values:
# Check for missing values
dataset.isna().any()
entry_id False
age False
pay_schedule False
home_owner False
income False
months_employed False
years_employed False
current_address_year False
personal_account_m False
personal_account_y False
has_debt False
amount_requested False
risk_score False
risk_score_2 False
risk_score_3 False
risk_score_4 False
risk_score_5 False
ext_quality_score False
ext_quality_score_2 False
inquiries_last_month False
e_signed False
dtype: bool
Fortunately, this dataset is clean, with no missing entries.
With a clean dataset, we can proceed to visualize the distribution of numerical features and assess their relationship with our response variable, e_signed.
Visualizing Feature Distributions with Histograms
Histograms allow us to understand how each feature is distributed across all applicants, highlighting any potential skewness or unique patterns. To focus on relevant features, we remove non-numeric columns, such as entry_id, pay_schedule, and the response variable e_signed, from the dataset before plotting:
# Dropping non-numeric columns
dataset2 = dataset.drop(columns=['entry_id', 'pay_schedule', 'e_signed'])
# Plotting histograms
fig = plt.figure(figsize=(15, 12))
plt.suptitle('Histograms of Numerical Columns', fontsize=20)
for i in range(dataset2.shape[1]):
plt.subplot(6, 3, i + 1)
f = plt.gca()
f.set_title(dataset2.columns.values[i])
vals = np.size(dataset2.iloc[:, i].unique())
if vals >= 100:
vals = 100
plt.hist(dataset2.iloc[:, i], bins=vals, color='#3F5D7D')
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()
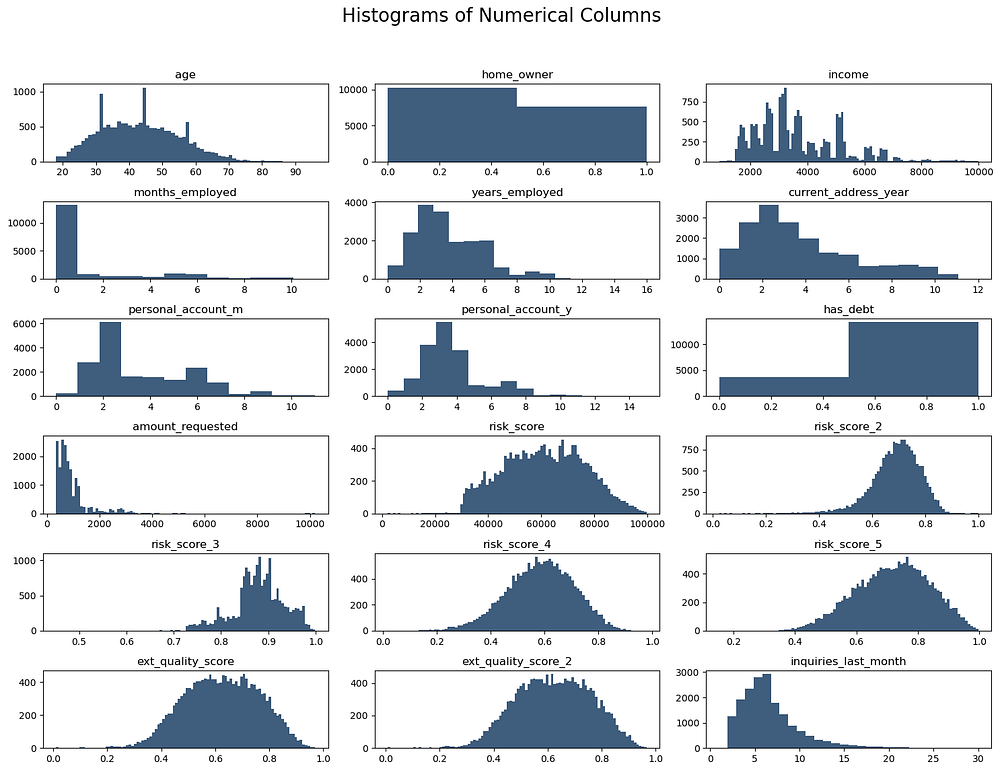
Age: Fairly evenly distributed among applicants aged 20–70, with some peaks around 30–50.
Home_owner: Binary distribution with slightly more non-homeowners (0) than homeowners (1).
Income: Right-skewed, with most applicants earning between $2,000 and $5,000 monthly.
Months_employed: The majority are at 0, indicating many are new to their jobs or unemployed.
Years_employed: Distributed up to 16 years, with a peak of around 3–5 years.
Current_address_year: Right-skewed, with most people living at their address for fewer than 6 years.
Personal_account_m and Personal_account_y: Indicate varying account age, with peaks at specific intervals.
Has_debt: Most applicants (about 80%) have debt.
Amount_requested: Most loan requests are under $2,000, with a long right tail.
Risk and Quality Scores: Risk and external quality scores (except
risk_score) show normal distributions, centred around 0.5-0.8.Inquiries_last_month: Right-skewed, with most applicants having fewer than 5 inquiries.
In summary, Months Employed was dropped due to an unusual and potentially flawed distribution, while Inquiries Last Month and Amount Requested showed skewed distributions but were retained as they may hold predictive value.
Correlation with Response Variable
To better understand how individual features relate to the likelihood of completing the e-sign step, we plot the correlation of each feature with e_signed. This helps identify which features have the strongest influence on the target variable:
# Correlation plot with e_signed/target variable
dataset2.corrwith(dataset['e_signed']).plot.bar(
figsize=(20, 10), title="Correlation with E Signed", fontsize=15, rot=45, grid=True
)
# Correlation table
corr_table = pd.DataFrame(
{'Feature': dataset2.columns.values,
'Correlation with E Signed': dataset2.corrwith(dataset['e_signed'])}
)
print(corr_table.sort_values(by='Correlation with E Signed', ascending=False))
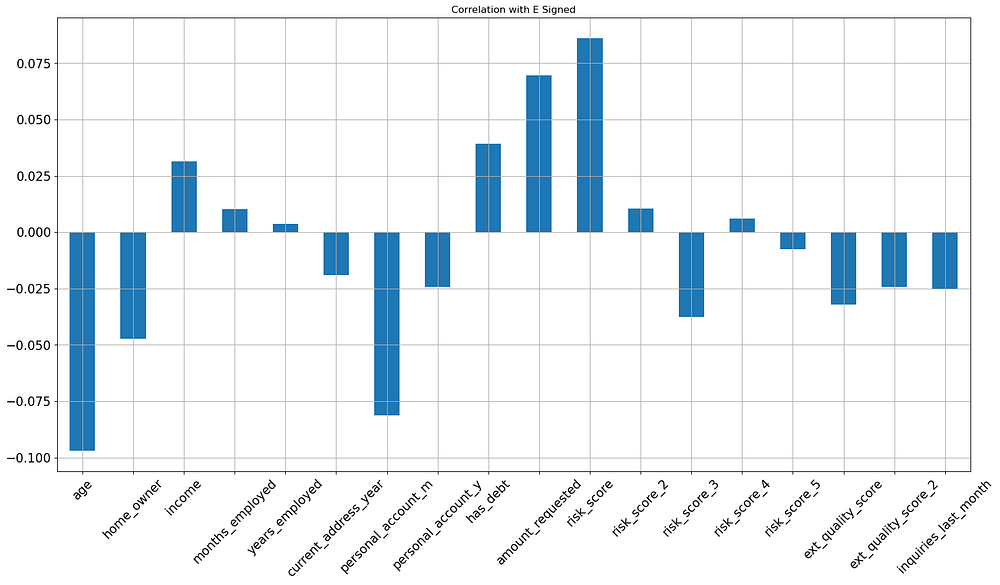
Feature Correlation with E Signed
risk_score risk_score 0.086098
amount_requested amount_requested 0.069572
has_debt has_debt 0.039192
income income 0.031377
risk_score_2 risk_score_2 0.010473
months_employed months_employed 0.010128
risk_score_4 risk_score_4 0.006147
years_employed years_employed 0.003748
risk_score_5 risk_score_5 -0.007541
current_address_year current_address_year -0.018969
personal_account_y personal_account_y -0.024160
ext_quality_score_2 ext_quality_score_2 -0.024271
inquiries_last_month inquiries_last_month -0.025165
ext_quality_score ext_quality_score -0.032129
risk_score_3 risk_score_3 -0.037483
home_owner home_owner -0.047409
personal_account_m personal_account_m -0.081195
age age -0.096998
Positive Correlations:
risk_score,amount_requested,has_debt, andincomeshow the highest positive correlations withe_signed, indicating that applicants with higher risk scores, loan amounts, debt, and income are slightly more likely to complete the e-sign step.
Negative Correlations:
age,personal_account_m, andhome_ownerhave the strongest negative correlations, suggesting that older applicants, those with longer personal account histories, and homeowners are less likely to e-sign.ext_quality_score,risk_score_3, andinquiries_last_monthalso show weak negative correlations withe_signed, indicating a slight decrease in e-sign likelihood with higher values in these features.
Overall, financial engagement metrics like risk_score and amount_requested slightly encourage e-signing, while demographic indicators like age and homeownership decrease it. However, all correlations are relatively weak, suggesting no single feature is a strong predictor on its own.
Correlation Matrix
To understand how features interrelate, we examine the full correlation matrix. This helps ensure that highly correlated features don’t introduce redundancy, which could affect model performance. For visualization, we use a heatmap to make it easier to identify strongly correlated feature pairs:
# Correlation matrix heatmap
corr = dataset2.corr()
mask = np.zeros_like(corr, dtype=bool)
mask[np.triu_indices_from(mask)] = True
f, ax = plt.subplots(figsize=(18, 15))
cmap = sns.diverging_palette(220, 10, as_cmap=True)
sns.heatmap(corr, mask=mask, cmap=cmap, vmax=.3, center=0,
square=True, linewidths=.5, cbar_kws={"shrink": .5},
annot=corr.round(2), fmt='.2f')
plt.show()
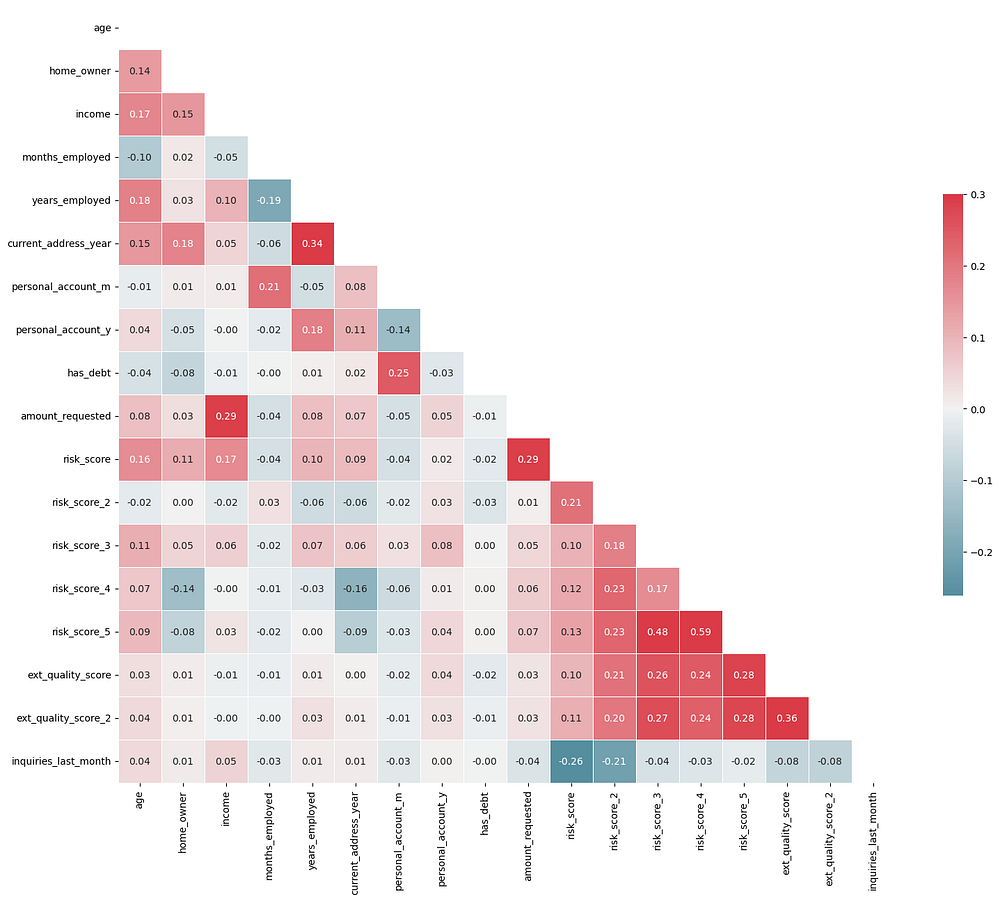
Interpretation:
Low Correlations Overall:
Most feature pairs have correlations well below 0.3, indicating that each feature provides relatively unique information about the dataset.
This lack of high correlation suggests that there’s little risk of multicollinearity, meaning all features can likely be retained without negatively impacting model stability.
Moderate Positive Correlations:
Income and Amount Requested: With a correlation of 0.29, applicants with higher incomes tend to request larger loan amounts. Although noticeable, this moderate correlation is not high enough to suggest redundancy.
Years Employed and Current Address Year: This pair has a correlation of 0.34, implying that applicants with longer employment histories also tend to stay longer at a single address. However, this level of correlation still does not indicate multicollinearity, though it hints at some overlap in representing applicant stability.
Risk Score Features:
There are moderate correlations among some
risk_scorefeatures, with values ranging up to 0.59 betweenrisk_scoreandrisk_score_5. While this is the highest correlation observed, it is still below the threshold typically associated with multicollinearity.Given the overall moderate nature of these correlations, it may not be necessary to drop any
risk_scorefeatures, though dimensionality reduction could be considered if model performance later suggests it.
Insights on Individual Features:
Personal Account Duration:
personal_account_yandpersonal_account_mhave a low correlation of 0.18. Since they both reflect the account's duration in years and months, it might be practical to combine them into a single feature representing the total account duration in months, though it is not required by correlation standards.Inquiries Last Month and Risk Scores: The feature
inquiries_last_monthshows a mild negative correlation withrisk_score(-0.26), suggesting that applicants with more recent credit inquiries might have slightly lower risk scores. This relationship is modest and doesn’t indicate redundancy.
Overall, the heatmap reveals no strong correlations among the features, with most values well below 0.6*. This suggests low multicollinearity, allowing you to retain all features in the model without concern. The data appears well-suited for modeling without the need for feature elimination based on correlation.*
4. Data Preprocessing and Feature Engineering
In this section, we’ll prepare the data for modeling by handling any necessary preprocessing tasks and creating new features that may enhance the model’s predictive power. For this loan e-sign prediction project, the preprocessing and feature engineering steps are as follows:
Dropping Irrelevant or Faulty Features
Upon examining the data, we identified one feature that was not useful:
- Months Employed: This feature displayed an unusual distribution, with most values clustered at zero, likely due to data reporting issues. As it did not provide meaningful information, it was removed from the dataset to improve model accuracy.
# Dropping 'months_employed' due to lack of meaningful data
dataset = dataset.drop(columns=['months_employed'])
Combining Features for Better Representation
Two features, personal_account_m (months) and personal_account_y (years), both describe the duration for which the applicant has held a personal account. Instead of keeping these as separate columns, we combined them to create a single feature, personal_account_months, which provides the total account age in months.
# Creating a unified 'personal_account_months' feature
dataset['personal_account_months'] = dataset['personal_account_y'] * 12 + dataset['personal_account_m']
# Dropping the original columns to avoid redundancy
dataset = dataset.drop(columns=['personal_account_y', 'personal_account_m'])
Encoding Categorical Variables
The dataset contains one categorical feature, pay_schedule, which indicates the applicant’s pay frequency (e.g., weekly, bi-weekly). To include this in the model, we applied one-hot encoding using pd.get_dummies() to convert each pay frequency category into a binary column. Additionally, we removed one of the encoded columns to avoid the dummy variable trap, ensuring the columns remain linearly independent.
# One-hot encoding 'pay_schedule' and dropping one level to avoid dummy variable trap
dataset = pd.get_dummies(dataset, columns=['pay_schedule'], drop_first=True)
Separating the Target Variable
The target variable in this analysis is e_signed, which indicates whether or not an applicant completed the e-signing step. We separated e_signed from the other features to facilitate model training and evaluation.
# Separating the target variable from the features
X = dataset.drop(columns=['e_signed', 'entry_id']) # Features
y = dataset['e_signed'] # Target
Feature Scaling
Since the dataset contains features with varying scales (e.g., income, risk_score, and amount_requested), we standardized the data to bring all numerical features to a similar scale. This is especially important for algorithms sensitive to feature magnitude, such as logistic regression and support vector machines. We used StandardScaler from Scikit-Learn to scale the features.
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
Train-Test Split
To evaluate the model’s performance, we split the dataset into training and testing sets, with 80% of the data used for training and 20% for testing. This split allows us to train the model on one portion of the data and validate it on another, providing a realistic measure of its accuracy.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=0)
Summary: After data preprocessing and feature engineering, we have a cleaned, well-prepared dataset with standardized features and one-hot encoded categorical variables, ready for model building. By removing redundant or unhelpful features and scaling the data, we aim to improve the model’s ability to accurately predict whether an applicant will complete the e-signing process.
5. Model Selection and Training
In our project, we used three different models to predict the likelihood of a loan applicant completing the e-signing process: Logistic Regression, Support Vector Machine (SVM) with an RBF kernel, and Random Forest. To streamline the training and evaluation of these models, we employed an Object-Oriented Programming (OOP) approach, which allowed us to reduce redundancy and make the code more organized and efficient.
We created a ModelEvaluator class to handle training, prediction, and performance evaluation consistently across models. This class enabled us to run each model through the same evaluation process and compare their performance metrics easily.
Here’s how the ModelEvaluator class was structured and used:
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, confusion_matrix
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
class ModelEvaluator:
def __init__(self, model, model_name):
self.model = model
self.model_name = model_name
def train(self, X_train, y_train):
self.model.fit(X_train, y_train)
def evaluate(self, X_test, y_test):
y_pred = self.model.predict(X_test)
# Calculate metrics
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)
# Display the results
print(f"{self.model_name} Performance:")
print("Accuracy:", accuracy)
print("Precision:", precision)
print("Recall:", recall)
print("F1 Score:", f1)
# Display confusion matrix
print("Confusion Matrix:\n", confusion_matrix(y_test, y_pred))
# Return results for further analysis if needed
return accuracy, precision, recall, f1
# Define models with names
log_reg = ModelEvaluator(LogisticRegression(penalty='l1', solver='liblinear', random_state=0), "Logistic Regression")
svm_linear = ModelEvaluator(SVC(kernel='linear', random_state=0), "SVM (Linear Kernel)")
svm_rbf = ModelEvaluator(SVC(kernel='rbf', random_state=0), "SVM (RBF Kernel)")
rf = ModelEvaluator(RandomForestClassifier(n_estimators=100, criterion='entropy', random_state=0), "Random Forest")
# Train and evaluate each model
log_reg.train(X_train, y_train)
log_reg.evaluate(X_test, y_test)
svm_linear.train(X_train, y_train)
svm_linear.evaluate(X_test, y_test)
svm_rbf.train(X_train, y_train)
svm_rbf.evaluate(X_test, y_test)
rf.train(X_train, y_train)
rf.evaluate(X_test, y_test)
Logistic Regression Performance:
Accuracy: 0.5628140703517588
Precision: 0.5766299745977985
Recall: 0.7064315352697096
F1 Score: 0.634965034965035
Confusion Matrix:
[[ 654 1000]
[ 566 1362]]
SVM (Linear Kernel) Performance:
Accuracy: 0.5683975432719152
Precision: 0.5777687296416938
Recall: 0.7359958506224067
F1 Score: 0.6473540145985401
Confusion Matrix:
[[ 617 1037]
[ 509 1419]]
SVM (RBF Kernel) Performance:
Accuracy: 0.5971524288107203
Precision: 0.6107811786203746
Recall: 0.6934647302904564
F1 Score: 0.649502064610153
Confusion Matrix:
[[ 802 852]
[ 591 1337]]
Random Forest Performance:
Accuracy: 0.6228364042434394
Precision: 0.6409379579872985
Recall: 0.6804979253112033
F1 Score: 0.660125786163522
Confusion Matrix:
[[ 919 735]
[ 616 1312]]
Here’s the table summarizing the performance metrics of each model:
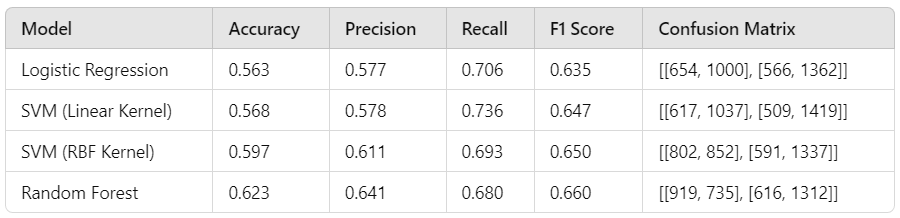
Interpretation
Random Forest achieved the highest accuracy (62.3%) and F1 score (0.660), suggesting it’s the best performer among the four models for balancing both precision and recall.
SVM with RBF Kernel came next with an accuracy of 59.7% and an F1 score of 0.650, showing a more balanced performance than SVM with a linear kernel.
SVM (Linear Kernel) showed a relatively higher recall (73.6%) but lower accuracy and F1 score than the RBF Kernel, suggesting it captures true positives well but has lower precision.
Logistic Regression had the lowest accuracy (56.3%) and F1 score, indicating it may be less effective for this dataset compared to the other models.
In summary, Random Forest appears most suitable for further tuning and cross-validation, with SVM (RBF Kernel) as a potential alternative if performance improvements are needed.
6. Hyperparameter Tuning with Grid Search
After selecting Random Forest as the best-performing model, we applied two rounds of Grid Search combined with K-Fold Cross-Validation to fine-tune its hyperparameters. This multi-step approach allowed us to improve performance by first exploring a broad range of values and then refining the parameter grid.
Process
- First Round of Grid Search: In the first round, we defined a broad range of hyperparameters for Random Forest to capture general trends:
n_estimators: [50, 100, 150]max_depth: [None, 10, 20, 30]min_samples_leaf: [1, 2, 4]criterion: ['gini', 'entropy']
We performed 10-fold cross-validation within Grid Search, which evaluated each combination across 10 different splits of the data. This provided a robust estimate of model performance for each configuration.
2. Second Round of Grid Search: Based on the first round’s results, we refined the hyperparameter grid, focusing on the most promising values:
If the best
n_estimatorswas 100, we adjusted the range to [90, 100, 110].Similarly,
max_depthandmin_samples_leafwere refined to values close to the optimal ones found in the first round.
This second round further narrowed down the configuration to achieve the best performance while maintaining efficiency.
Here’s the code used to conduct the two rounds of Grid Search:
from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestClassifier
# First round of Grid Search with a broader range
rf_param_grid_1 = {
'n_estimators': [50, 100, 150],
'max_depth': [None, 10, 20, 30],
'min_samples_leaf': [1, 2, 4],
'criterion': ['gini', 'entropy']
}
# Initialize the Random Forest model
rf = RandomForestClassifier(random_state=0)
# First round of Grid Search
rf_grid_search_1 = GridSearchCV(estimator=rf, param_grid=rf_param_grid_1, cv=10, scoring='accuracy', n_jobs=-1)
rf_grid_search_1.fit(X_train, y_train)
# Extract best parameters from the first round
best_params_1 = rf_grid_search_1.best_params_
# Refined parameter grid for the second round based on first round results
rf_param_grid_2 = {
'n_estimators': [best_params_1['n_estimators'] - 10, best_params_1['n_estimators'], best_params_1['n_estimators'] + 10],
'max_depth': [best_params_1['max_depth'] - 2, best_params_1['max_depth'], best_params_1['max_depth'] + 2] if best_params_1['max_depth'] else [None],
'min_samples_leaf': [max(1, best_params_1['min_samples_leaf'] - 1), best_params_1['min_samples_leaf'], best_params_1['min_samples_leaf'] + 1],
'criterion': [best_params_1['criterion']]
}
# Second round of Grid Search
rf_grid_search_2 = GridSearchCV(estimator=rf, param_grid=rf_param_grid_2, cv=10, scoring='accuracy', n_jobs=-1)
rf_grid_search_2.fit(X_train, y_train)
# Output the best parameters and best cross-validated accuracy
print("Best Parameters for Random Forest:", rf_grid_search_2.best_params_)
print("Best Cross-Validation Accuracy:", rf_grid_search_2.best_score_)
Best Parameters for Random Forest: {'n_estimators': 100, 'max_depth': None, 'min_samples_leaf': 2, 'criterion': 'entropy'}
Best Cross-Validation Accuracy: 0.638
Explanation:
Best Parameters: The grid search selected a configuration with:
n_estimators: 100 (indicating 100 trees in the forest)max_depth: None (meaning no limit to the depth of each tree, allowing trees to grow until all leaves are pure or contain fewer samples thanmin_samples_leaf)min_samples_leaf: 2 (meaning each leaf node must contain at least 2 samples)criterion: 'entropy' (indicating that entropy is used to measure the quality of a split)
Best Cross-Validation Accuracy: Approximately 63.8% accuracy, which aligns with the mentioned cross-validated accuracy score.
Confusion matrix
The final step will be using a confusion matrix to access the final model:
from sklearn.metrics import confusion_matrix, classification_report
# Use the best Random Forest model from Grid Search to make predictions on the test set
y_pred = rf_grid_search_2.best_estimator_.predict(X_test)
# Generate the confusion matrix
conf_matrix = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:\n", conf_matrix)
# Generate the classification report for precision, recall, F1-score, and accuracy
class_report = classification_report(y_test, y_pred)
print("Classification Report:\n", class_report)
Classification Report:
precision recall f1-score support
0 0.60 0.56 0.58 1654
1 0.64 0.68 0.66 1928
accuracy 0.62 3582
macro avg 0.62 0.62 0.62 3582
weighted avg 0.62 0.62 0.62 3582
This confusion matrix and classification report offer insight into the Random Forest’s classification effectiveness:
Class 1 (e-signed) has a higher recall than Class 0 (non-e-signed), indicating the model is better at identifying e-sign completions.
The F1 scores show that the model has a moderate balance between precision and recall.
7. Conclusion and business implications
The completion of this project brings valuable insights into how predictive modeling can significantly enhance the onboarding experience in FinTech. By using our Random Forest model to predict the likelihood of a loan applicant completing the e-signature process, we gain a practical tool for optimizing customer interactions and boosting business outcomes.
Using Model Predictions to Optimize the Onboarding Experience
With our model’s predictions, the company can strategically adjust the onboarding process. For applicants predicted to be less likely to complete the e-sign phase, we can implement targeted interventions, such as customized follow-ups, tailored content, or proactive assistance. This approach ensures that each applicant receives an optimized experience suited to their level of engagement, increasing the likelihood that they complete the onboarding process.
Business Impact: Enhanced Loan Conversions and Profits
This predictive capability can drive direct business impact. Improving e-sign completion rates directly increases the likelihood of loan conversions, allowing the company to process more successful applications. This increase in conversions not only enhances customer satisfaction but also positively affects the company’s bottom line, ultimately leading to a greater return on marketing investments and overall profitability.
Summary of the Modeling Process
Our modeling journey focused on developing a balanced approach between technical rigor and business relevance:
Data Exploration and Preprocessing: Analyzed and cleaned the data to ensure quality inputs.
Feature Engineering: Optimized feature selection for accurate model predictions.
Model Selection and Tuning: Tested multiple models, then fine-tuned our Random Forest model through grid search and cross-validation, balancing model accuracy and interpretability.
Evaluation and Interpretation: Used precision, recall, and F1 scores to assess model effectiveness and understand how predictions translate into business action.
This balance of technical accuracy and business insight illustrates the real value of data science in business, allowing us to make data-driven decisions with measurable impact.
Key Takeaways and Future Directions
This project demonstrates that even straightforward predictive models, like a Random Forest classifier, can yield valuable insights that enhance both customer experience and profitability. By refining the onboarding process based on data-driven predictions, we make it easier for customers to complete their applications while maximizing potential revenue.
Looking forward, there are opportunities to improve this model further. Incorporating more complex algorithms (such as neural networks) or using larger datasets could improve accuracy and uncover deeper insights. Additionally, including more behavioral and demographic features may reveal new patterns that could further enhance targeting strategies.
In fintech, where small improvements can yield large impacts, the insights from this model mark a meaningful step toward a more efficient, customer-centered onboarding experience.
Appendices
Data source: https://www.kaggle.com/datasets/aniruddhachoudhury/esigning-of-loan-based-on-financial-history
