---

1. Introduction

Gold has long been a valuable asset, playing a crucial role in investment portfolios and financial markets. Its price often reflects economic conditions, making accurate forecasting an essential tool for investors and analysts. In this project, we harness the power of machine learning to predict gold prices using historical data and various economic indicators.

By analyzing and modeling data, we aim to uncover patterns and trends that influence gold price fluctuations. This hands-on guide will walk you through the process of using Python and Streamlit to build and deploy a predictive model, leveraging the gold price dataset from Kaggle.

2. Problem Definition and Data Overview

Problem Definition

The primary challenge is to accurately predict the price of gold based on historical data and related economic factors. With fluctuations in global markets and changing economic conditions, the ability to forecast gold prices is a valuable skill for investors and financial planners.

Our goal in this project is twofold:

1. Develop a machine learning model that predicts gold prices with high accuracy.

2. Deploy the model using Streamlit for easy accessibility and real-time usage.

Accurate predictions can assist stakeholders in making informed investment decisions, mitigating risks, and capitalizing on market opportunities.

Data introduction

The dataset consists of 2,290 rows and 6 columns, with each row representing a specific date and the corresponding values of various economic indicators. The columns and their meanings are as follows:

1. Date: The date corresponding to the recorded data (non-numerical, used for time-series analysis).

2. SPX: The S&P 500 Index, a benchmark for stock market performance. Higher values indicate a strong stock market.

3. GLD: The gold price (target variable), measured in US dollars. It represents the value of gold at the respective date.

4. USO: A measure of crude oil prices, represented by the United States Oil Fund. It reflects the energy market trends.

5. SLV: The silver price, measured in US dollars. It shows the value of silver, often correlated with gold prices.

6. EUR/USD: The Euro-to-US Dollar exchange rate, indicating currency market trends.

Initial Observations

• SPX and EUR/USD values reflect broader economic and market conditions that may indirectly influence gold prices.

• USO, SLV, and GLD capture commodity trends, with potential interdependencies among them.

• Gold prices range between 70.00 and 184.59, with an average value of 122.73, highlighting significant variability over time.

This overview provides critical context for the dataset, helping us understand the relationships between features and their potential impact on the target variable, GLD.

3. Exploratory Data Analysis (EDA)

Exploratory Data Analysis (EDA) is a crucial step in understanding the dataset’s structure and uncovering insights that drive the model-building process. In this project, we analyze the gold price dataset to identify patterns and correlations that could influence price predictions.

Dataset Overview

To get started, we load the dataset and examine its structure using Python’s pandas library:

# Load the dataset
users_data = pd.read_csv('gld_price_data.csv')

# Check the structure of the dataset
print(users_data.info())
print(users_data.describe())

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 2290 entries, 0 to 2289
Data columns (total 6 columns):
 #   Column   Non-Null Count  Dtype  
---  ------   --------------  -----  
 0   Date     2290 non-null   object 
 1   SPX      2290 non-null   float64
 2   GLD      2290 non-null   float64
 3   USO      2290 non-null   float64
 4   SLV      2290 non-null   float64
 5   EUR/USD  2290 non-null   float64
dtypes: float64(5), object(1)
memory usage: 107.5+ KB
None
               SPX          GLD          USO          SLV      EUR/USD
count  2290.000000  2290.000000  2290.000000  2290.000000  2290.000000
mean   1654.315776   122.732875    31.842221    20.084997     1.283653
std     519.111540    23.283346    19.523517     7.092566     0.131547
min     676.530029    70.000000     7.960000     8.850000     1.039047
25%    1239.874969   109.725000    14.380000    15.570000     1.171313
50%    1551.434998   120.580002    33.869999    17.268500     1.303297
75%    2073.010070   132.840004    37.827501    22.882500     1.369971
max    2872.870117   184.589996   117.480003    47.259998     1.598798
       Date          SPX        GLD        USO     SLV   EUR/USD
0  1/2/2008  1447.160034  84.860001  78.470001  15.180  1.471692
1  1/3/2008  1447.160034  85.570000  78.370003  15.285  1.474491
2  1/4/2008  1411.630005  85.129997  77.309998  15.167  1.475492
3  1/7/2008  1416.180054  84.769997  75.500000  15.053  1.468299
4  1/8/2008  1390.189941  86.779999  76.059998  15.590  1.557099

The dataset overview provides the following insights:

1. Structure:

• The dataset contains 2,290 rows and 6 columns: Date, SPX, GLD, USO, SLV, and EUR/USD.

• The Date column is of type object, while the other five columns are numerical (float64).

2. Data Quality: All columns have non-null values, indicating no missing data.

3. Descriptive Statistics:

SPX (S&P 500 Index):

• Mean: 1,654.32, Std. Dev: 519.11

• Wide range between Min (676.53) and Max (2,872.87), indicating high variability in the S&P 500 Index.

GLD (Gold Price):

• Mean: 122.73, Std. Dev: 23.28

• Values range from 70.00 to 184.59, reflecting significant variations in gold prices.

USO (Oil Fund):

• Mean: 31.84, Std. Dev: 19.52

• Large range from 7.96 to 117.48, highlighting volatility in oil prices.

SLV (Silver Price):

• Mean: 20.08, Std. Dev: 7.09

• Values span 8.85 to 47.26, showing moderate variability in silver prices.

EUR/USD (Currency Exchange Rate):

• Mean: 1.28, Std. Dev: 0.13

• A narrow range from 1.04 to 1.60, indicating relative stability compared to other variables.

4. Initial Observations:

• GLD likely has correlations with other variables (SPX, USO, SLV, EUR/USD) due to their economic interdependencies.

• High variability in SPX, USO, and SLV may reflect their influence on gold price movements.

• Consistent data quality (no null values) ensures smooth preprocessing and modeling.

This analysis sets the stage for exploring correlations and trends during EDA to identify patterns influencing gold price predictions.

Visualizing Gold Price Trends

To explore trends in the data, we visualize the gold prices over time:

import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from matplotlib.ticker import MaxNLocator

# Plot gold prices over time
plt.figure(figsize=(12, 6))
plt.plot(users_data['Date'], users_data['GLD'], label='Gold Price', color='gold')

# Format the x-axis to show more dense date labels
plt.gca().xaxis.set_major_locator(mdates.MonthLocator(interval=3))  # Set ticks every 3 months
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m'))

# Rotate the date labels for better readability
plt.xticks(rotation=45)
plt.title('Gold Price Trend Over Time')
plt.xlabel('Date')
plt.ylabel('Gold Price')
plt.legend()
plt.tight_layout()
plt.show()

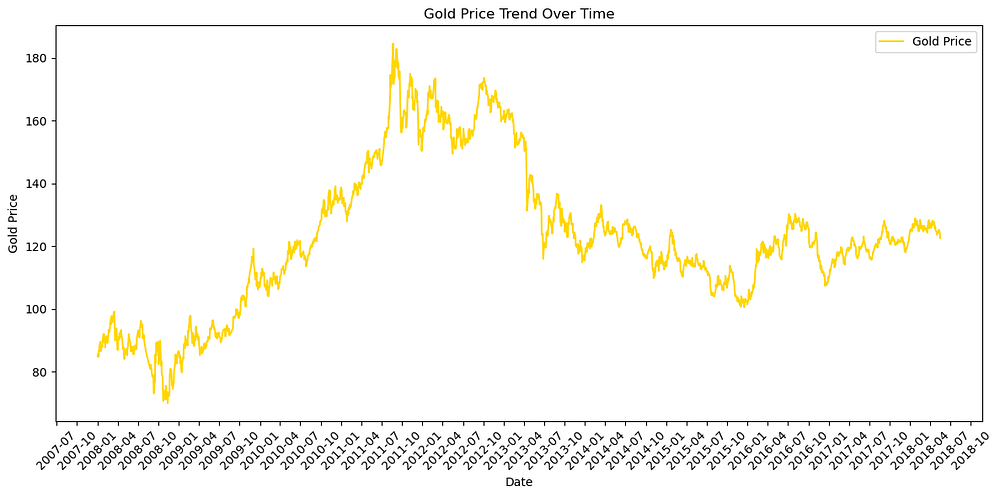
The plot displays the trend of gold prices over time, highlighting the following key observations:

1. Overall Growth: Gold prices exhibit a significant upward trend, peaking around 2012, which reflects a period of heightened value for gold in the global market.

2. Volatility: The plot reveals substantial fluctuations, particularly during the rapid increase leading to the peak and the subsequent decline.

3. Stabilization: From 2014 onward, gold prices show a more stable pattern with moderate variations.

This analysis provides a comprehensive view of gold price movements over the years, setting the stage for further exploration of factors influencing these trends.

Correlation Analysis

Understanding relationships between features is critical for feature selection. A correlation heatmap helps identify how strongly features are related to GLD:

# Exclude the 'Date' column before calculating correlations
correlation_matrix = users_data.drop(columns=['Date']).corr()

# Plot the heatmap
import seaborn as sns
import matplotlib.pyplot as plt

plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', fmt='.2f')
plt.title('Correlation Heatmap (Excluding Date)')
plt.show()

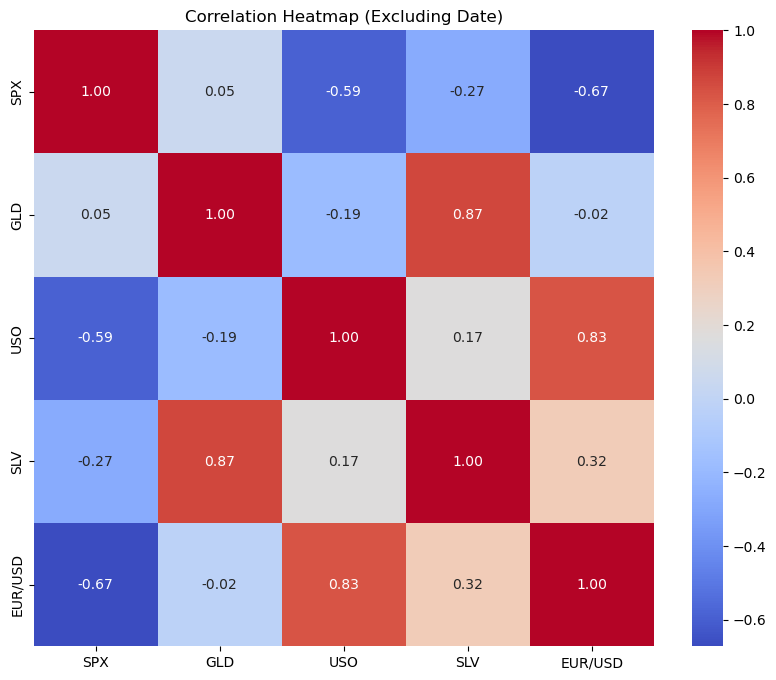
This heatmap shows the correlation between numerical features in the dataset, excluding the Date column. Key observations include:

1. Strong Correlation: GLD (gold price) has a strong positive correlation with SLV (silver price) (0.87), indicating a close relationship between gold and silver markets.

2. Negative Correlations:

• SPX (S&P 500 Index) and GLD show a weak positive correlation (0.05), suggesting little dependence between them.

• EUR/USD and SPX have a strong negative correlation (-0.67), indicating an inverse relationship between the exchange rate and the stock market index.

3. Notable Relationships: USO (oil prices) correlates moderately with EUR/USD (0.83) and weakly with GLD (-0.19), reflecting some indirect connections to gold prices.

These insights help identify which features are likely to influence gold prices and guide feature selection for model building.

4. Data Preprocessing

Data preprocessing is a critical step in preparing the dataset for machine learning modeling. It involves cleaning the data, handling missing values, and transforming features into a format suitable for analysis and modeling. For this project, the following preprocessing steps were applied:

Handling Missing Values

The dataset was first checked for missing values using the .isnull().sum() method:

# Check for missing values
print(users_data.isnull().sum())

Date       0
SPX        0
GLD        0
USO        0
SLV        0
EUR/USD    0
dtype: int64

Upon inspection, no missing values were found in the dataset. This ensures that no imputation or removal of rows is necessary, simplifying the preprocessing step.

Feature Scaling

Since the dataset contains features with different units and ranges (e.g., GLD in USD, SPX as an index, and EUR/USD as an exchange rate), feature scaling was applied to standardize the values. This ensures that no feature disproportionately influences the machine learning models:

from sklearn.preprocessing import StandardScaler

# Selecting numerical features (excluding 'Date')
features = users_data.drop(columns=['Date'])
scaler = StandardScaler()
scaled_features = scaler.fit_transform(features)

# Convert scaled features back to a DataFrame
scaled_data = pd.DataFrame(scaled_features, columns=features.columns)

Splitting Data into Features and Target

The target variable, GLD (gold price), was separated from the other features for model training:

# Separate features and target
X = scaled_data.drop(columns=['GLD'])
y = scaled_data['GLD']

Splitting Data into Training and Testing Sets

To evaluate the model’s performance, the dataset was divided into training and testing sets using an 80–20 split:

from sklearn.model_selection import train_test_split

# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

These preprocessing steps lay the foundation for building accurate and robust predictive models for gold prices.

5. Feature Engineering

Since the Exploratory Data Analysis (EDA) already highlighted the relationships between features and the target variable GLD, we focus here on ensuring the dataset is optimized for model building. The key steps include:

Retaining All Features Initially

While SLV (silver price) and other features like USO (oil prices) and EUR/USD (exchange rate) are more strongly correlated with GLD, we retain all features (SPX, USO, SLV, EUR/USD) for the initial model training to avoid prematurely discarding potentially useful information.

Feature Importance

Instead of relying solely on correlation, we leverage feature importance from models like Random Forest to evaluate which features contribute most to predicting GLD. This analysis will be performed during the model evaluation step.

6. Model Building and Evaluation

Model building involves training machine learning algorithms to predict gold prices. Here’s how the process is structured:

Models Used

We train three machine learning models to predict GLD:

1. Linear Regression: A baseline model to capture linear relationships between features and the target.

2. Random Forest Regressor: An ensemble model that effectively handles non-linear relationships and feature interactions.

3. Gradient Boosting Regressor: A sequential learning model that minimizes errors over multiple iterations.

Model Training

Each model is trained on the training set (X_train, y_train) and evaluated on the test set (X_test, y_test).

Linear Regression

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

# Train Linear Regression
lr_model = LinearRegression()
lr_model.fit(X_train, y_train)

# Predict and evaluate
y_pred_lr = lr_model.predict(X_test)
print("Linear Regression R^2 Score:", r2_score(y_test, y_pred_lr))
print("Linear Regression RMSE:", mean_squared_error(y_test, y_pred_lr, squared=False))

Linear Regression R^2 Score: 0.8975640982991402
Linear Regression RMSE: 0.32194718826931107

Random Forest Regressor

from sklearn.ensemble import RandomForestRegressor

# Train Random Forest
rf_model = RandomForestRegressor(random_state=42)
rf_model.fit(X_train, y_train)

# Predict and evaluate
y_pred_rf = rf_model.predict(X_test)
print("Random Forest R^2 Score:", r2_score(y_test, y_pred_rf))
print("Random Forest RMSE:", mean_squared_error(y_test, y_pred_rf, squared=False))

Random Forest R^2 Score: 0.9899859327093791
Random Forest RMSE: 0.10066159135413218

Gradient Boosting Regressor

from sklearn.ensemble import GradientBoostingRegressor

# Train Gradient Boosting
gb_model = GradientBoostingRegressor(random_state=42)
gb_model.fit(X_train, y_train)

# Predict and evaluate
y_pred_gb = gb_model.predict(X_test)
print("Gradient Boosting R^2 Score:", r2_score(y_test, y_pred_gb))
print("Gradient Boosting RMSE:", mean_squared_error(y_test, y_pred_gb, squared=False))

Gradient Boosting R^2 Score: 0.9802596392786268
Gradient Boosting RMSE: 0.14133056051673887

Model Comparison

The performance of three machine learning models — Linear Regression, Random Forest, and Gradient Boosting — was evaluated using two metrics: R² Score and Root Mean Squared Error (RMSE). Below are the results:

1. Linear Regression (R² Score: 0.8976, RMSE: 0.3219): Linear Regression provides a baseline performance with an R² score of 89.76%, indicating it explains most of the variability in the gold prices. However, the RMSE is relatively high compared to the other models, suggesting that the predictions are less accurate.

2. Random Forest (R² Score: 0.9900, RMSE: 0.1007): Random Forest demonstrates the best performance among all models. With an R² score of 99.00%, it captures almost all variability in the data. The low RMSE value highlights its high prediction accuracy, making it the most suitable model for this task.

3. Gradient Boosting (R² Score: 0.9803, RMSE: 0.1413): Gradient Boosting performs well, with an R² score of 98.03%, slightly below Random Forest. The RMSE is also higher than that of Random Forest but lower than Linear Regression, indicating good accuracy with slightly less robustness compared to Random Forest.

Overall, based on the evaluation:

• Random Forest emerges as the best-performing model with the highest R² score and the lowest RMSE, making it the most reliable choice for predicting gold prices.

• Gradient Boosting offers a strong alternative, especially for scenarios requiring a lighter model than Random Forest.

• Linear Regression, while decent, is outperformed by the ensemble models in terms of both explanatory power and prediction accuracy.

The Random Forest model will be used in the deployment phase for real-time predictions.

8. Deployment and Practical Use

To make the gold price prediction model accessible and practical, we deployed the Random Forest model using Streamlit, a lightweight web application framework for Python. This allows users to interact with the model in real time and predict gold prices based on input features.

Saving the Model in main.py

After training the Random Forest model in your main script, save it using the joblib library:

import joblib

# Save the trained model to a pickle file
joblib.dump(rf_model, 'random_forest_model.pkl')
print("Model saved as 'random_forest_model.pkl'")

Setting Up Streamlit

Streamlit was chosen for deployment due to its simplicity and efficiency in creating interactive web applications. To install Streamlit, use the following command:

pip install streamlit

Creating the Streamlit App

The app accepts user inputs for features such as SPX, USO, SLV, and EUR/USD and predicts the gold price (GLD). Below is a sample code snippet for the app:

import streamlit as st
import numpy as np
import pandas as pd
import joblib  # For loading the trained model

# Load the trained Random Forest model
model = joblib.load('random_forest_model.pkl')

# Streamlit app title
st.title("Gold Price Prediction App")

# Input fields for feature values
st.sidebar.header("Input Features")
spx = st.sidebar.number_input("S&P 500 Index (SPX)", value=1650.0, step=1.0)
uso = st.sidebar.number_input("Crude Oil Price (USO)", value=30.0, step=1.0)
slv = st.sidebar.number_input("Silver Price (SLV)", value=20.0, step=0.1)
eur_usd = st.sidebar.number_input("EUR/USD Exchange Rate", value=1.3, step=0.01)

# Predict button
if st.button("Predict Gold Price"):
    # Create a DataFrame with the input values
    input_data = pd.DataFrame({
        'SPX': [spx],
        'USO': [uso],
        'SLV': [slv],
        'EUR/USD': [eur_usd]
    })

    # Make a prediction
    prediction = model.predict(input_data)
    st.success(f"Predicted Gold Price: ${prediction[0]:.2f}")

Running the App

To run the app locally, navigate to the directory containing your script and execute the following command:

streamlit run app.py

This launches the app in your default browser, where you can input values for the features and get real-time predictions for gold prices.

The app after deployment will look like this:

Practical Use

This app can be used by:

• Investors: To predict gold prices and make informed investment decisions.

• Analysts: To analyze market conditions and their impact on gold prices.

• Educational Purposes: As a learning tool for understanding the application of machine learning in financial forecasting.

9. Conclusion

In this project, we explored the process of predicting gold prices using machine learning techniques. By leveraging a dataset with historical gold prices and economic indicators, we developed and deployed a predictive model. The project encompassed key steps, including Exploratory Data Analysis (EDA), data preprocessing, feature engineering, model building, and deployment using Streamlit.

The Random Forest model emerged as the best-performing model, achieving an R² score of 99.00% and a Root Mean Squared Error (RMSE) of 0.1007, making it a robust choice for predicting gold prices. The deployment via Streamlit provided a user-friendly interface, enabling real-time predictions based on input features.

This project highlights the practical applications of machine learning in financial forecasting and demonstrates how to build, evaluate, and deploy models effectively. The approach can be extended to other financial assets or predictive tasks, providing valuable insights for investors, analysts, and educators.

By combining machine learning with deployment tools like Streamlit, we can bridge the gap between complex models and real-world usability, making data-driven predictions accessible to a broader audience.

---

Appendices

Code: https://github.com/Minhhoang2606/Gold-price-prediction-by-machine-learning

Data source: https://www.kaggle.com/datasets/altruistdelhite04/gold-price-data/data