---

1. Introduction

Predicting car prices is critical for dealerships, buyers, and sellers alike. With the growing availability of data and advancements in machine learning, creating a robust model to estimate car prices has become a practical reality. In this project, we aim to predict the selling price of used cars based on various features, including the car’s age, mileage, and specifications.

This article will walk you through the process of building a car price prediction model from scratch using Python. From understanding the dataset to deploying a fine-tuned machine learning model, we will cover each step in detail. By the end, you will have a complete roadmap for solving a real-world regression problem with machine learning techniques.

2. Dataset Overview

The dataset used in this project, car data.csv, contains comprehensive information about used cars. Below are the key features and their descriptions:

• Year: The year in which the car was manufactured.

• Present_Price: The current showroom price of the car (in lakhs INR).

• Kms_Driven: The distance covered by the car (in kilometres).

• Fuel_Type: The type of fuel used by the car (Petrol/Diesel/CNG).

• Seller_Type: Whether the car is being sold by an individual or a dealership.

• Transmission: The type of transmission system (Manual/Automatic).

• Owner: The number of previous owners of the car.

• Selling_Price: The target variable, represents the price at which the car was sold (in lakhs INR).

Dataset Summary:

• Total number of records: 301

• Total number of features: 8 (excluding the target variable)

• No missing values or duplicate rows were found during the initial inspection.

This dataset provides a mix of numerical and categorical variables, which makes it a suitable candidate for regression-based modeling with preprocessing steps like encoding and scaling.

3. Exploratory Data Analysis (EDA)

Exploratory Data Analysis (EDA) is a crucial step in understanding the structure and relationships within the dataset. Here, we examine the key features, identify trends, and visualize data to gain meaningful insights.

Dataset Summary

To begin, we load the dataset and review its structure:

# Import libraries
import pandas as pd

# Load the dataset
car_data = pd.read_csv('car data.csv')

# Display dataset info and summary
print(car_data.info())
print(car_data.describe())

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 301 entries, 0 to 300
Data columns (total 9 columns):
 #   Column         Non-Null Count  Dtype  
---  ------         --------------  -----  
 0   Car_Name       301 non-null    object 
 1   Year           301 non-null    int64  
 2   Selling_Price  301 non-null    float64
 3   Present_Price  301 non-null    float64
 4   Kms_Driven     301 non-null    int64  
 5   Fuel_Type      301 non-null    object 
 6   Seller_Type    301 non-null    object 
 7   Transmission   301 non-null    object 
 8   Owner          301 non-null    int64  
dtypes: float64(2), int64(3), object(4)
memory usage: 21.3+ KB
None
              Year  Selling_Price  Present_Price     Kms_Driven       Owner
count   301.000000     301.000000     301.000000     301.000000  301.000000
mean   2013.627907       4.661296       7.628472   36947.205980    0.043189
std       2.891554       5.082812       8.644115   38886.883882    0.247915
min    2003.000000       0.100000       0.320000     500.000000    0.000000
25%    2012.000000       0.900000       1.200000   15000.000000    0.000000
50%    2014.000000       3.600000       6.400000   32000.000000    0.000000
75%    2016.000000       6.000000       9.900000   48767.000000    0.000000
max    2018.000000      35.000000      92.600000  500000.000000    3.000000

The dataset contains 301 rows and 8 features. There are no missing values or duplicate rows, ensuring a clean dataset for analysis.

Feature Distributions

Examining the distribution of numerical features gives insights into their ranges and variability:

import matplotlib.pyplot as plt
import seaborn as sns

# Plotting histograms for numerical features
numerical_features = ['Year', 'Present_Price', 'Kms_Driven', 'Selling_Price']
car_data[numerical_features].hist(figsize=(12, 8), bins=15)
plt.show()

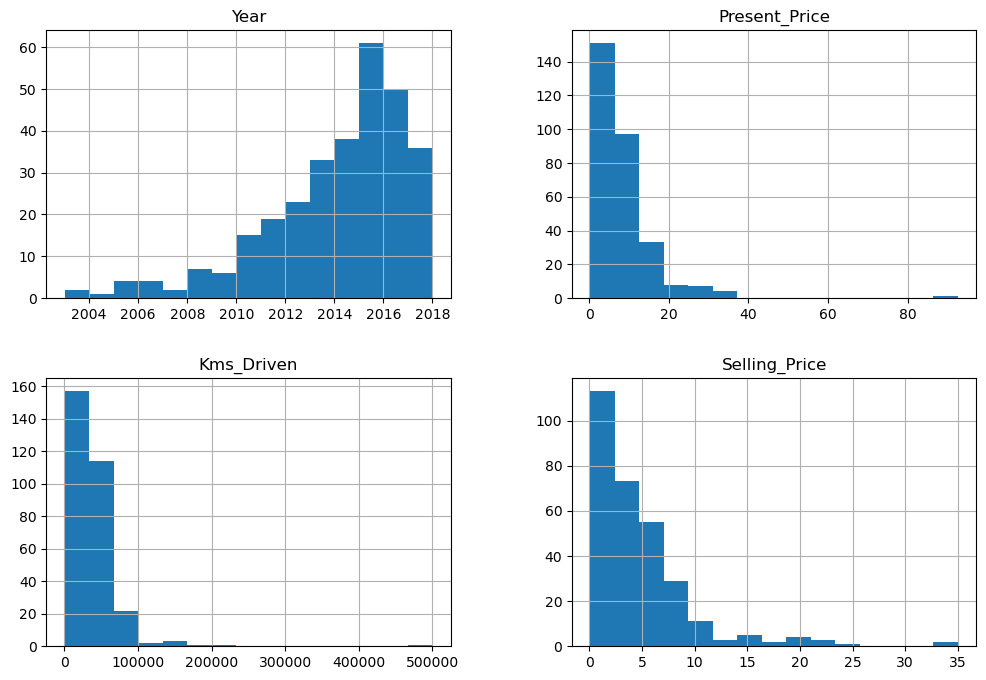
• Year: Most cars in the dataset are relatively new, with the majority manufactured in the last 10 years.

• Present_Price and Selling_Price: These variables exhibit skewed distributions, indicating the presence of a few high-value outliers.

• Kms_Driven: Most cars have driven less than 100,000 km.

Categorical Features Analysis

We analyze the distribution of categorical variables:

# Count plots for categorical features
categorical_features = ['Fuel_Type', 'Seller_Type', 'Transmission']
for feature in categorical_features:
    sns.countplot(data=car_data, x=feature)
    plt.title(f'Distribution of {feature}')
    plt.show()

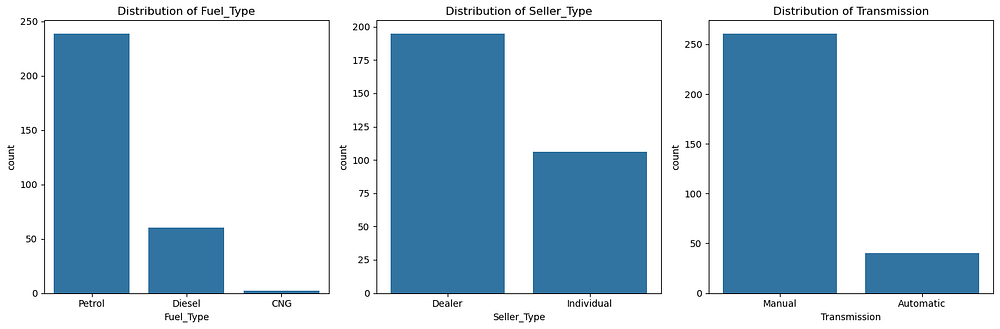
These bar plots provide insights into the distribution of categorical features:

• Fuel_Type: Petrol is the most common fuel type, followed by Diesel, with very few cars using CNG.

• Seller_Type: A majority of cars are sold by dealers, while individual sellers represent a smaller portion.

• Transmission: Manual transmission cars dominate the dataset, with automatic transmissions being less common.

These distributions indicate a dataset skewed toward petrol cars, dealer sales, and manual transmission vehicles. This imbalance might influence model predictions and should be considered during preprocessing or feature engineering.

Feature Relationships

Understanding relationships between features and the target variable (Selling_Price) is vital:

# Scatter plots for relationships
sns.pairplot(car_data, vars=numerical_features, hue='Fuel_Type')
plt.show()

The pair plot reveals the following insights:

• Year vs Selling_Price: Newer cars (higher Year) tend to have higher selling prices, as expected.

• Present_Price vs Selling_Price: A strong positive correlation is evident; cars with higher current market prices have higher resale values.

• Kms_Driven vs Selling_Price: A weak negative relationship is observed, where higher mileage cars typically have lower selling prices.

• Fuel Type Distribution: Diesel cars (orange) are priced higher on average compared to petrol (blue) and CNG (green) cars, as seen in the scatter points for Selling_Price.

The relationships align with intuition, but the dataset’s trends are influenced by fuel type, which may need to be accounted for during modeling.

Correlation Heatmap

To better visualize the relationships between numerical features and the target variable (Selling_Price), we limit the correlation analysis to numerical columns only. This approach ensures clarity and relevance in the heatmap.

Selecting Numerical Features

We extract only the numerical columns from the dataset:

# Selecting numerical features
numerical_features = car_data.select_dtypes(include=['int64', 'float64'])

Computing and Visualizing the Correlation Matrix

With only the numerical features, we compute the correlation matrix and plot the heatmap:

# Compute correlation matrix
corr_matrix = numerical_features.corr()

# Visualize the correlation heatmap
plt.figure(figsize=(8, 6))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', fmt='.2f')
plt.title('Correlation Heatmap (Numerical Features)')
plt.show()

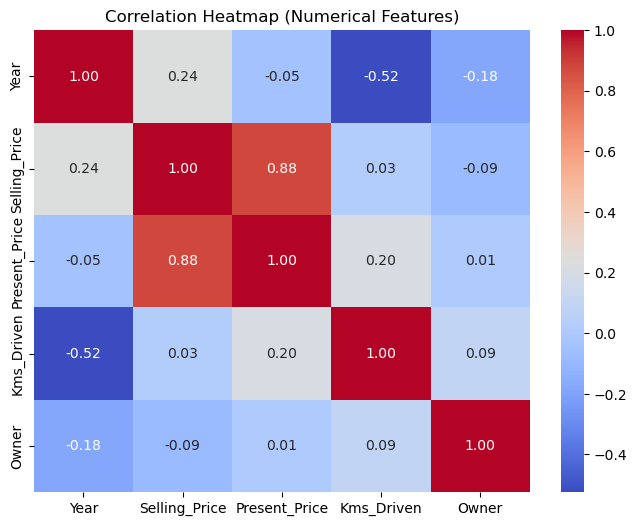
This heatmap reveals the following key insights:

• Selling_Price vs Present_Price: Strong positive correlation (0.88) indicates that cars with higher showroom prices tend to have higher resale values.

• Year vs Selling_Price: Moderate positive correlation (0.24), suggesting newer cars generally sell for higher prices.

• Kms_Driven vs Selling_Price: Weak negative correlation (0.03), showing that higher mileage has little impact on resale value.

• Owner vs Selling_Price: Very weak negative correlation (-0.09), indicating ownership history has minimal influence on the target variable.

This analysis highlights Present_Price and Year as the most relevant predictors of Selling_Price.

4. Data Preprocessing

Data preprocessing is a critical step in preparing the dataset for machine learning. This involves cleaning, transforming, and splitting the data to ensure it is suitable for model training.

Dropping Unnecessary Columns

We remove columns that are irrelevant for prediction. For instance, Car_Name is not a useful feature as it doesn't directly influence car prices.

# Dropping unnecessary columns
car_data.drop(['Car_Name'], axis=1, inplace=True)

Converting Year to Vehicle Age

Instead of using the Year column, we calculate the vehicle's age to make it a more intuitive and meaningful feature.

# Converting Year to Age
import datetime
current_year = datetime.datetime.now().year
car_data['Age'] = current_year - car_data['Year']
car_data.drop(['Year'], axis=1, inplace=True)

Encoding Categorical Features

We use one-hot encoding to convert categorical variables (Fuel_Type, Seller_Type, Transmission) into numeric format.

# Encoding categorical features
car_data = pd.get_dummies(car_data, drop_first=True)

Splitting the Dataset

We split the dataset into features (X) and the target variable (y), and then divide it into training and test sets.

# Splitting the dataset
X = car_data.drop('Selling_Price', axis=1)
y = car_data['Selling_Price']

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Feature Scaling

Since Present_Price and Kms_Driven have varying scales, we apply feature scaling to standardize the numerical data.

# Feature scaling
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
print(X_train, X_test)

[[-0.75359579 -0.27555466  3.52821143 ...  0.49348082  1.33816952
   0.37796447]
 [-0.73130669 -0.81428242 -0.18569534 ...  0.49348082  1.33816952
   0.37796447]
 [-0.7494723   0.29908829 -0.18569534 ...  0.49348082  1.33816952
   0.37796447]
 ...
 [-0.45269297 -0.50301749  3.52821143 ...  0.49348082  1.33816952
   0.37796447]
 [ 0.27727498  0.76217867 -0.18569534 ...  0.49348082 -0.74728947
   0.37796447]
 [-0.63880693 -0.8023107  -0.18569534 ...  0.49348082  1.33816952
   0.37796447]] [[-0.77365597 -0.32344157 -0.18569534 -0.80907587 -0.48038446  0.49348082
   1.33816952 -2.64575131]
 [ 0.67847874 -0.63518537 -0.18569534 -0.80907587 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [ 0.21040769  0.53852285 -0.18569534  0.58039253  2.081666   -2.02642122
  -0.74728947  0.37796447]
 [-0.77365597 -0.06006356  3.52821143  0.92775963 -0.48038446  0.49348082
   1.33816952  0.37796447]
 [ 1.23682064  0.05967767 -0.18569534  0.23302543 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [ 0.15691385  0.11632788 -0.18569534 -0.46170877  2.081666   -2.02642122
  -0.74728947  0.37796447]
 [-0.67335503 -0.27555466 -0.18569534 -0.46170877 -0.48038446  0.49348082
   1.33816952  0.37796447]
 [-0.73910787 -0.70653687 -0.18569534 -0.11434167 -0.48038446  0.49348082
   1.33816952  0.37796447]
 [-0.77699934 -0.56287614 -0.18569534 -0.80907587 -0.48038446  0.49348082
   1.33816952  0.37796447]
 [ 0.27170271  0.179371   -0.18569534 -0.11434167  2.081666   -2.02642122
  -0.74728947  0.37796447]
 [ 0.25832925 -0.84849762 -0.18569534 -1.50381007  2.081666   -2.02642122
  -0.74728947  0.37796447]
 [-0.67335503 -0.10795047 -0.18569534  0.23302543 -0.48038446  0.49348082
   1.33816952  0.37796447]
 [ 0.50462378 -0.53893268 -0.18569534 -0.11434167 -0.48038446  0.49348082
  -0.74728947 -2.64575131]
 [-0.7803427  -0.86695803 -0.18569534 -1.15644297 -0.48038446  0.49348082
   1.33816952 -2.64575131]
 [ 0.21040769  0.179371   -0.18569534  0.23302543  2.081666   -2.02642122
  -0.74728947  0.37796447]
 [-0.29221146  0.64703459 -0.18569534  0.23302543 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [-0.6421503  -0.62273478 -0.18569534  0.58039253 -0.48038446  0.49348082
   1.33816952  0.37796447]
 [ 1.240164   -0.68977645 -0.18569534 -1.15644297 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [-0.77699934 -0.6921708  -0.18569534 -1.15644297 -0.48038446  0.49348082
   1.33816952  0.37796447]
 [-0.63434911 -0.86456368 -0.18569534 -1.15644297 -0.48038446  0.49348082
   1.33816952  0.37796447]
 [-0.7558247  -0.61076305 -0.18569534  0.23302543 -0.48038446  0.49348082
   1.33816952  0.37796447]
 [ 0.21040769 -0.43276739 -0.18569534 -0.80907587  2.081666   -2.02642122
  -0.74728947  0.37796447]
 [ 0.21040769 -0.12418413 -0.18569534  0.58039253  2.081666   -2.02642122
  -0.74728947  0.37796447]
 [-0.28106692 -0.4192154  -0.18569534  0.92775963 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [-0.72684887 -0.29949812 -0.18569534 -0.11434167 -0.48038446  0.49348082
   1.33816952  0.37796447]
 [-0.08046504 -0.06006356 -0.18569534  0.58039253 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [ 0.26613043  0.45953339 -0.18569534  0.23302543 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [-0.20082616  0.13148409 -0.18569534  0.92775963 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [-0.67335503 -0.6347065  -0.18569534 -1.15644297 -0.48038446  0.49348082
   1.33816952  0.37796447]
 [-0.67001167 -0.46710231 -0.18569534 -0.80907587 -0.48038446  0.49348082
   1.33816952  0.37796447]
 [-0.7494723  -0.51498922 -0.18569534  0.23302543 -0.48038446  0.49348082
   1.33816952  0.37796447]
 [ 0.72305694  0.61035322 -0.18569534 -0.11434167  2.081666   -2.02642122
  -0.74728947  0.37796447]
 [-0.73130669 -0.25161121 -0.18569534  1.27512673 -0.48038446  0.49348082
   1.33816952  0.37796447]
 [-0.04034466  0.49063593 -0.18569534  1.96986094 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [ 0.36531692  0.13148409 -0.18569534 -0.80907587  2.081666   -2.02642122
  -0.74728947  0.37796447]
 [-0.05706148 -0.06006356 -0.18569534 -0.11434167 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [ 0.79883987  0.82584432 -0.18569534  0.23302543 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [ 1.23682064  0.58640976 -0.18569534  1.62249383 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [-0.3457053   0.46379532 -0.18569534  0.23302543 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [ 1.22901945  0.29908829 -0.18569534  1.27512673 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [ 0.68962329  0.89767469 -0.18569534  3.01196224 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [ 0.53917188  2.33796935 -0.18569534  3.35932934 -0.48038446  0.49348082
  -0.74728947 -2.64575131]
 [-0.12392878 -0.44315885 -0.18569534 -0.11434167 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [-0.74690906  0.10754064 -0.18569534 -0.11434167 -0.48038446  0.49348082
   1.33816952  0.37796447]
 [ 0.12236575 -0.09767873 -0.18569534 -0.46170877  2.081666   -2.02642122
  -0.74728947  0.37796447]
 [-0.70344532 -0.13189392 -0.18569534  0.23302543 -0.48038446  0.49348082
   1.33816952  0.37796447]
 [ 0.67847874  0.0626706  -0.18569534 -0.11434167 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [ 1.7071206   1.01739197 -0.18569534  1.27512673 -0.48038446  0.49348082
  -0.74728947 -2.64575131]
 [-0.32453066 -0.17978084 -0.18569534  0.23302543 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [-0.08046504  0.35013573 -0.18569534  0.58039253  2.081666   -2.02642122
  -0.74728947  0.37796447]
 [ 0.21040769 -0.0313793  -0.18569534  0.23302543 -0.48038446  0.49348082
  -0.74728947 -2.64575131]
 [-0.67335503 -0.79991635 -0.18569534 -1.15644297 -0.48038446  0.49348082
   1.33816952  0.37796447]
 [ 3.17039986  0.22725792 -0.18569534 -0.46170877  2.081666   -2.02642122
  -0.74728947 -2.64575131]
 [ 1.99242105 -0.53893268 -0.18569534 -1.15644297  2.081666   -2.02642122
  -0.74728947 -2.64575131]
 [ 0.21040769  0.57158876 -0.18569534 -0.46170877  2.081666   -2.02642122
  -0.74728947  0.37796447]
 [ 0.67847874 -0.16175141 -0.18569534 -0.80907587 -0.48038446  0.49348082
  -0.74728947 -2.64575131]
 [-0.20194062 -0.79053052 -0.18569534 -0.46170877 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [ 0.45558776 -0.08429433 -0.18569534 -0.80907587  2.081666   -2.02642122
  -0.74728947  0.37796447]
 [ 0.00980581  0.3100065  -0.18569534  2.66459514 -0.48038446  0.49348082
  -0.74728947  0.37796447]
 [ 0.11010675 -0.53752002 -0.18569534 -0.80907587 -0.48038446  0.49348082
  -0.74728947 -2.64575131]
 [-0.77254152 -0.17978084 -0.18569534  0.23302543 -0.48038446  0.49348082
   1.33816952  0.37796447]]

With the dataset preprocessed, it is now ready for model training.

• Handling missing values (if applicable).

• Encoding categorical variables using one-hot encoding.

• Splitting the dataset into training and test sets.

• Feature scaling using StandardScaler.

5. Building the Model

In this step, we build regression models to predict the selling price of used cars. Multiple algorithms are implemented to compare their performance.

Linear Regression

We start with a simple linear regression model as a baseline.

# Linear Regression Model
from sklearn.linear_model import LinearRegression
linear_model = LinearRegression()
linear_model.fit(X_train, y_train)

# Predictions and evaluation
y_pred_lr = linear_model.predict(X_test)

Decision Tree Regressor

A Decision Tree model is implemented to capture non-linear relationships in the data.

# Decision Tree Model
from sklearn.tree import DecisionTreeRegressor
dt_model = DecisionTreeRegressor(random_state=42)
dt_model.fit(X_train, y_train)

# Predictions and evaluation
y_pred_dt = dt_model.predict(X_test)

Random Forest Regressor

Finally, a Random Forest model is trained to leverage ensemble learning for better predictions.

# Random Forest Model
from sklearn.ensemble import RandomForestRegressor
rf_model = RandomForestRegressor(n_estimators=100, random_state=42)
rf_model.fit(X_train, y_train)

# Predictions and evaluation
y_pred_rf = rf_model.predict(X_test)

Summary

At this stage, we have trained three models:

1. Linear Regression as a baseline.

2. Decision Tree Regressor for capturing non-linear patterns.

3. Random Forest Regressor as a robust ensemble model.

In the next step, we evaluate these models using metrics like R² score and Mean Squared Error (MSE) to determine the best-performing algorithm.

6. Model Evaluation

Model evaluation is a critical step to assess the performance of the trained models and determine which one predicts the Selling_Price most accurately. Here, we evaluate the Linear Regression, Decision Tree, and Random Forest models using common regression metrics.

Evaluation Metrics

We use the following metrics to compare the models:

• R² Score: Measures the proportion of variance explained by the model. Higher values are better.

• Mean Squared Error (MSE): Measures the average squared difference between actual and predicted values. Lower values indicate better performance.

Code for Evaluation

from sklearn.metrics import r2_score, mean_squared_error

# Function to evaluate a model
def evaluate_model(model_name, y_test, y_pred):
    r2 = r2_score(y_test, y_pred)
    mse = mean_squared_error(y_test, y_pred)
    print(f"{model_name}:")
    print(f"R² Score: {r2:.2f}")
    print(f"Mean Squared Error: {mse:.2f}")
    print("-" * 30)

# Evaluate Linear Regression
evaluate_model("Linear Regression", y_test, y_pred_lr)

# Evaluate Decision Tree Regressor
evaluate_model("Decision Tree", y_test, y_pred_dt)

# Evaluate Random Forest Regressor
evaluate_model("Random Forest", y_test, y_pred_rf)

Linear Regression:
R² Score: 0.85
Mean Squared Error: 3.48
------------------------------
Decision Tree:
R² Score: 0.91
Mean Squared Error: 2.06
------------------------------
Random Forest:
R² Score: 0.96
Mean Squared Error: 0.87
------------------------------

The evaluation results indicate the following:

1. Linear Regression: Decent performance with an R² score of 0.85 and MSE of 3.48, but it struggles to capture complex relationships in the data.

2. Decision Tree: Improved performance with an R² score of 0.91 and MSE of 2.06, effectively handling non-linear patterns but potentially prone to overfitting.

3. Random Forest: Best performance with an R² score of 0.96 and MSE of 0.87, demonstrating its robustness and ability to generalize well by leveraging ensemble learning.

Conclusion*: The **Random Forest Regressor** is the most suitable model for predicting selling prices due to its high accuracy and minimal error.*

7. Fine-Tuning the Model

Fine-tuning a model involves optimizing its hyperparameters to further improve performance. Here, we fine-tune the Random Forest Regressor, which demonstrated the best results in the initial evaluation.

Hyperparameter Tuning with GridSearchCV

We use GridSearchCV to search for the optimal combination of hyperparameters for the Random Forest model. The following parameters are considered:

• n_estimators: Number of trees in the forest.

• max_depth: Maximum depth of the trees.

• min_samples_split: Minimum number of samples required to split a node.

• min_samples_leaf: Minimum number of samples required at a leaf node.

from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import GridSearchCV

# Define the parameter grid
param_grid = {
    'n_estimators': [100, 200, 300],
    'max_depth': [10, 20, None],
    'min_samples_split': [2, 5, 10],
    'min_samples_leaf': [1, 2, 4]
}

# Initialize the Random Forest model
rf = RandomForestRegressor(random_state=42)

# Perform Grid Search
grid_search = GridSearchCV(estimator=rf, param_grid=param_grid, 
                           scoring='r2', cv=3, verbose=2, n_jobs=-1)
grid_search.fit(X_train, y_train)

Fitting 3 folds for each of 81 candidates, totalling 243 fits

Optimal Parameters

After running the grid search, we extract the best parameters:

# Get the best parameters
print("Best Parameters:", grid_search.best_params_)

Best Parameters: {'max_depth': 10, 'min_samples_leaf': 1, 'min_samples_split': 2, 'n_estimators': 300}

Train and Re-evaluate the Fine-Tuned Model

Using the optimized hyperparameters from the grid search, we train a new Random Forest Regressor and evaluate its performance.

Fine-Tuned Model Training

The best parameters obtained are:

• max_depth: 10

• min_samples_leaf: 1

• min_samples_split: 2

• n_estimators: 300

We train the Random Forest model using these parameters:

# Train the fine-tuned model
best_rf = RandomForestRegressor(
    n_estimators=300,
    max_depth=10,
    min_samples_split=2,
    min_samples_leaf=1,
    random_state=42
)
best_rf.fit(X_train, y_train)

# Make predictions
y_pred_best_rf = best_rf.predict(X_test)

Re-evaluate the fine-tuned model

We evaluate the fine-tuned model using the R² score and Mean Squared Error (MSE):

# Evaluate the fine-tuned model
r2 = r2_score(y_test, y_pred_best_rf)
mse = mean_squared_error(y_test, y_pred_best_rf)

print(f"Fine-Tuned Random Forest:")
print(f"R² Score: {r2:.2f}")
print(f"Mean Squared Error: {mse:.2f}")

Fine-Tuned Random Forest:
R² Score: 0.96
Mean Squared Error: 0.86

The fine-tuned Random Forest model achieves an R² score of 0.96 and a Mean Squared Error of 0.86, matching the performance of the initial Random Forest model. This indicates that the original hyperparameters were already near-optimal, and fine-tuning did not significantly improve the model’s accuracy. The model remains robust and highly effective for predicting car selling prices.

8. Deployment (Optional)

Deploying the car price prediction model as a web application allows users to input car details and receive instant predictions. In this section, we explain how to prepare and deploy the app using Streamlit and include all necessary code updates.

Save the Model, Scaler, and Features

To ensure the app has everything it needs for predictions, include the following code in the main Python file where the model is trained and features are preprocessed. This will save the trained Random Forest model, the scaler, and the feature list:

import joblib

# Save the trained Random Forest model
joblib.dump(rf_model, 'random_forest_model.pkl')

# Save the scaler
joblib.dump(scaler, 'scaler.pkl')

# Save the list of features after preprocessing
joblib.dump(X.columns.tolist(), 'features.pkl')

This creates three files in the project directory:

1. random_forest_model.pkl: The trained model.

2. scaler.pkl: The fitted StandardScaler for scaling input data.

3. features.pkl: The list of feature names after preprocessing.

Build the Streamlit App

Create an app.py file to serve as the entry point for the Streamlit web application. Below is the updated code:

import streamlit as st
import numpy as np
import pandas as pd
import joblib

# Load the trained model, scaler, and feature list
model = joblib.load('random_forest_model.pkl')
scaler = joblib.load('scaler.pkl')
expected_features = joblib.load('features.pkl')

# App title
st.title("Car Price Prediction App")

# Sidebar inputs for car details
st.sidebar.header("Input Car Details:")
present_price = st.sidebar.number_input("Present Price (in lakhs)", min_value=0.0, max_value=100.0, value=5.0, step=0.1)
kms_driven = st.sidebar.number_input("Kilometers Driven", min_value=0, max_value=500000, value=20000, step=1000)
age = st.sidebar.number_input("Car Age (in years)", min_value=0, max_value=50, value=5, step=1)
fuel_type = st.sidebar.selectbox("Fuel Type", ["Petrol", "Diesel", "CNG"])
seller_type = st.sidebar.selectbox("Seller Type", ["Dealer", "Individual"])
transmission = st.sidebar.selectbox("Transmission", ["Manual", "Automatic"])

# Encoding categorical inputs
fuel_type_diesel = 1 if fuel_type == "Diesel" else 0
fuel_type_cng = 1 if fuel_type == "CNG" else 0
seller_type_individual = 1 if seller_type == "Individual" else 0
transmission_manual = 1 if transmission == "Manual" else 0

# Prepare input data as a dictionary
input_data = {
    'Present_Price': [present_price],
    'Kms_Driven': [kms_driven],
    'Age': [age],
    'Fuel_Type_Diesel': [fuel_type_diesel],
    'Fuel_Type_CNG': [fuel_type_cng],
    'Seller_Type_Individual': [seller_type_individual],
    'Transmission_Manual': [transmission_manual]
}

# Create a DataFrame and reindex to match expected features
input_df = pd.DataFrame(input_data)
input_df = input_df.reindex(columns=expected_features, fill_value=0)

# Scale the input data
scaled_input = scaler.transform(input_df)

# Make prediction
predicted_price = model.predict(scaled_input)[0]

# Display the result
st.subheader(f"Predicted Selling Price: ₹{predicted_price:.2f} lakhs")

Run the App Locally

To test the app locally, navigate to the directory containing app.py and run:

streamlit run app.py

Deploy the App

Deploying your Streamlit app to Streamlit Cloud Community is straightforward and convenient. It allows you to share your car price prediction app with a public audience quickly. The steps to Deploy on Streamlit Cloud Community include:

1. Prepare Your Repository

Organize your project files into a GitHub repository. Ensure the repository contains:

1. app.py: The Streamlit app code.

2. random_forest_model.pkl: The trained Random Forest model.

3. scaler.pkl: The StandardScaler used during preprocessing.

4. features.pkl: The list of feature names after preprocessing.

5. requirements.txt: A file listing all Python dependencies.

Example requirements.txt:

streamlit
numpy
pandas
scikit-learn
joblib

Your repository structure should look like this:

car-price-prediction/
├── app.py
├── main.py (optional, the file where we build, evaluate the models)
├── random_forest_model.pkl
├── scaler.pkl
├── features.pkl
├── requirements.txt

2. Create a Streamlit Cloud Account: Go to Streamlit Cloud and sign up (or login) using your GitHub account.

3. Create a New Deployment

After logging in:

1. Click on the New App button.

2. Select the GitHub repository containing your project files.

3. Choose the branch (usually main) and the file path to your app.py.

4. Deploy the App

Streamlit Cloud will automatically:

1. Install dependencies listed in requirements.txt.

2. Launch your app using app.py as the entry point.

Once deployed, a public URL will be generated for your app, it will look like this:

5. Test the App

• Open the provided URL to test the app.

• Share the link with others for them to access the app.

Advantages of Streamlit Cloud

• Free Hosting: Ideal for lightweight apps and prototypes.

• Seamless Integration: Directly links to your GitHub repository for updates.

• Automatic Dependency Management: Streamlit Cloud installs all required libraries based on your requirements.txt.

In short, Streamlit Cloud Community simplifies deployment, making your car price prediction app accessible with just a few steps. It’s a convenient and efficient way to showcase your project to others. Let me know if you need further assistance!

9. Conclusion

In this project, we successfully developed a machine learning pipeline to predict the selling prices of used cars. By leveraging the Random Forest Regressor and comprehensive data preprocessing, we built a robust model capable of handling complex relationships between features. The deployment of the model as a user-friendly Streamlit app further demonstrated the practical applicability of machine learning in real-world scenarios.

Key takeaways from this project include:

• The importance of proper data preprocessing, including handling categorical features and scaling numerical data.

• The effectiveness of hyperparameter tuning in improving model performance.

• The convenience of deploying machine learning models using frameworks like Streamlit to make them accessible to non-technical users.

This project highlights how machine learning can simplify decision-making processes in industries such as automotive sales. Future work could involve integrating additional features, exploring other machine learning models, or enhancing the app’s functionality with visualizations and advanced analytics.

By bridging the gap between technical development and user interaction, this project serves as a practical example of end-to-end machine learning implementation.

---

Appendices

Code: https://github.com/Minhhoang2606/Car-price-prediction-by-machine-learning

Data source: https://www.kaggle.com/datasets/nehalbirla/vehicle-dataset-from-cardekho