Photo by Kostiantyn Li on Unsplash
Feature Engineering for Machine Learning: A Practical Guide Using the Ames Housing Dataset
1. Introduction
Feature engineering is a pivotal step in the machine learning pipeline. It transforms raw data into meaningful features that improve model performance, making it easier for algorithms to uncover patterns and make predictions. In this blog, we’ll dive into feature engineering using the Ames Housing Dataset, focusing on techniques applicable to linear regression and other machine learning models.
The Ames Housing Dataset is a rich dataset containing various characteristics of residential properties. It provides an excellent playground for applying and understanding feature engineering concepts. In this guide, we’ll walk through the process, from exploratory data analysis to transforming features for modeling. While the emphasis is on linear regression, these techniques can be adapted for other machine learning tasks.
Brief overview of feature engineering as a crucial step in machine learning pipelines.
Highlight the use of the Ames Housing Dataset and its relevance to linear regression and other models.
Mention the goal of transforming raw data into features that improve model performance.
2. Exploratory Data Analysis (EDA)
Before jumping into feature engineering, it’s crucial to understand the data. Let’s start by loading the Ames Housing Dataset and performing some basic exploratory data analysis.
Loading the Dataset
The dataset is stored in a .tsv (tab-separated values) file. Using Python’s Pandas library, we can load it with the following code:
import pandas as pd
# Load the dataset
df = pd.read_csv('data/Ames_Housing_Data1.tsv', sep='\t')
# Display the first few rows
print(df.head())
Order PID MS SubClass MS Zoning Lot Frontage Lot Area Street \
0 1 526301100 20 RL 141.0 31770 Pave
1 1 526301100 20 RL 141.0 31770 Pave
2 2 526350040 20 RH 80.0 11622 Pave
3 3 526351010 20 RL 81.0 14267 Pave
4 4 526353030 20 RL 93.0 11160 Pave
Alley Lot Shape Land Contour ... Pool Area Pool QC Fence Misc Feature \
0 NaN IR1 Lvl ... 0 NaN NaN NaN
1 NaN IR1 Lvl ... 0 NaN NaN NaN
2 NaN Reg Lvl ... 0 NaN MnPrv NaN
3 NaN IR1 Lvl ... 0 NaN NaN Gar2
4 NaN Reg Lvl ... 0 NaN NaN NaN
Misc Val Mo Sold Yr Sold Sale Type Sale Condition SalePrice
0 0 5 2010 WD Normal 215000
1 0 5 2010 WD Normal 215000
2 0 6 2010 WD Normal 105000
3 12500 6 2010 WD Normal 172000
4 0 4 2010 WD Normal 244000
[5 rows x 82 columns]
Here, sep='\t' specifies the tab separator, making it compatible with .tsv files.
Data Summary
Next, we use df.info() to get an overview of the dataset:
# Get an overview of the data
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 2931 entries, 0 to 2930
Data columns (total 82 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Order 2931 non-null int64
1 PID 2931 non-null int64
2 MS SubClass 2931 non-null int64
3 MS Zoning 2931 non-null object
4 Lot Frontage 2441 non-null float64
5 Lot Area 2931 non-null int64
6 Street 2931 non-null object
7 Alley 198 non-null object
8 Lot Shape 2931 non-null object
9 Land Contour 2931 non-null object
10 Utilities 2931 non-null object
11 Lot Config 2931 non-null object
12 Land Slope 2931 non-null object
13 Neighborhood 2931 non-null object
14 Condition 1 2931 non-null object
15 Condition 2 2931 non-null object
16 Bldg Type 2931 non-null object
17 House Style 2931 non-null object
18 Overall Qual 2931 non-null int64
19 Overall Cond 2931 non-null int64
20 Year Built 2931 non-null int64
21 Year Remod/Add 2931 non-null int64
22 Roof Style 2931 non-null object
23 Roof Matl 2931 non-null object
24 Exterior 1st 2931 non-null object
25 Exterior 2nd 2931 non-null object
26 Mas Vnr Type 1156 non-null object
27 Mas Vnr Area 2908 non-null float64
28 Exter Qual 2931 non-null object
29 Exter Cond 2931 non-null object
30 Foundation 2931 non-null object
31 Bsmt Qual 2851 non-null object
32 Bsmt Cond 2851 non-null object
33 Bsmt Exposure 2848 non-null object
34 BsmtFin Type 1 2851 non-null object
35 BsmtFin SF 1 2930 non-null float64
36 BsmtFin Type 2 2850 non-null object
37 BsmtFin SF 2 2930 non-null float64
38 Bsmt Unf SF 2930 non-null float64
39 Total Bsmt SF 2930 non-null float64
40 Heating 2931 non-null object
41 Heating QC 2931 non-null object
42 Central Air 2931 non-null object
43 Electrical 2930 non-null object
44 1st Flr SF 2931 non-null int64
45 2nd Flr SF 2931 non-null int64
46 Low Qual Fin SF 2931 non-null int64
47 Gr Liv Area 2931 non-null int64
48 Bsmt Full Bath 2929 non-null float64
49 Bsmt Half Bath 2929 non-null float64
50 Full Bath 2931 non-null int64
51 Half Bath 2931 non-null int64
52 Bedroom AbvGr 2931 non-null int64
53 Kitchen AbvGr 2931 non-null int64
54 Kitchen Qual 2931 non-null object
55 TotRms AbvGrd 2931 non-null int64
56 Functional 2931 non-null object
57 Fireplaces 2931 non-null int64
58 Fireplace Qu 1509 non-null object
59 Garage Type 2774 non-null object
60 Garage Yr Blt 2772 non-null float64
61 Garage Finish 2772 non-null object
62 Garage Cars 2930 non-null float64
63 Garage Area 2930 non-null float64
64 Garage Qual 2772 non-null object
65 Garage Cond 2772 non-null object
66 Paved Drive 2931 non-null object
67 Wood Deck SF 2931 non-null int64
68 Open Porch SF 2931 non-null int64
69 Enclosed Porch 2931 non-null int64
70 3Ssn Porch 2931 non-null int64
71 Screen Porch 2931 non-null int64
72 Pool Area 2931 non-null int64
73 Pool QC 13 non-null object
74 Fence 572 non-null object
75 Misc Feature 106 non-null object
76 Misc Val 2931 non-null int64
77 Mo Sold 2931 non-null int64
78 Yr Sold 2931 non-null int64
79 Sale Type 2931 non-null object
80 Sale Condition 2931 non-null object
81 SalePrice 2931 non-null int64
dtypes: float64(11), int64(28), object(43)
memory usage: 1.8+ MB
Visualizing Distributions
Exploring the distribution of variables is vital to detect patterns and outliers. For example, let’s examine the distribution of the Gr.Liv.Area (above-ground living area) column, which is known to contain outliers:
import matplotlib.pyplot as plt
# Plot a histogram of the Gr.Liv.Area column
df['Gr.Liv.Area'].hist(bins=50)
plt.title('Distribution of Gr.Liv.Area')
plt.xlabel('Gr.Liv.Area')
plt.ylabel('Frequency')
plt.show()
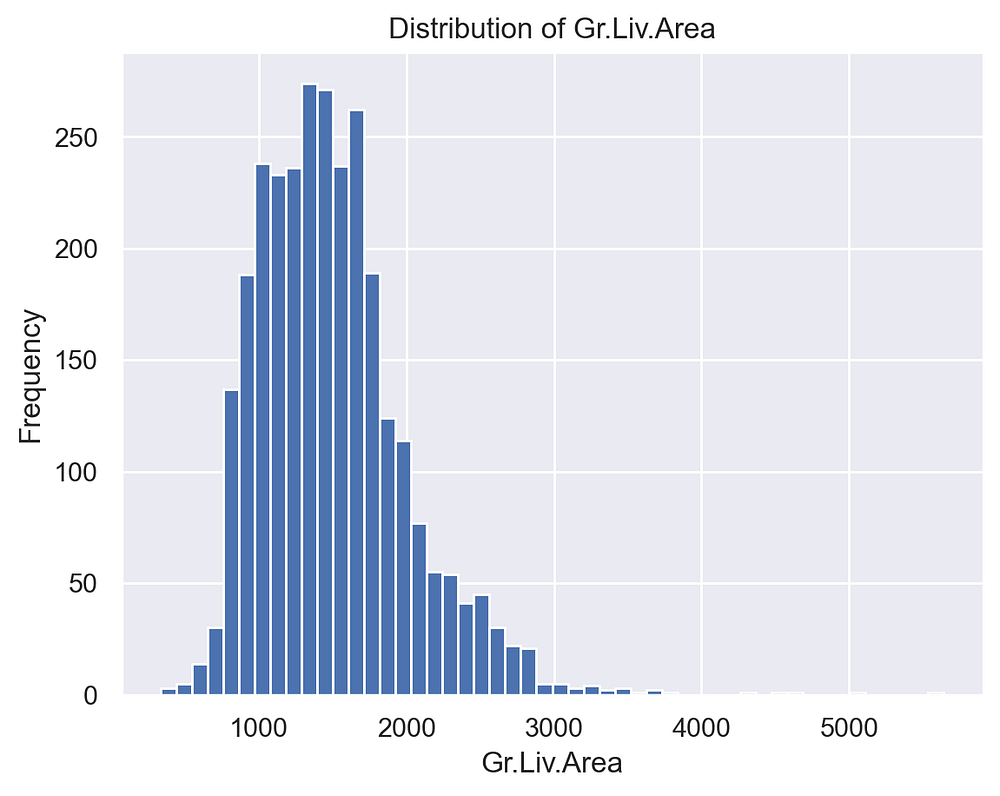
This visualization shows that most values lie below 4,000, with a few outliers beyond this range. These extreme values can skew our analysis, so we filter them out:
# Filter out rows where Gr.Liv.Area > 4000
df = df[df['Gr.Liv.Area'] <= 4000]
# Check the new shape of the dataset
print(df.shape)
(2926, 82)
3. Feature Selection
Feature selection is an essential step in feature engineering, helping to eliminate irrelevant or redundant features that add noise to the dataset. In the Ames Housing Dataset, we identified two columns, Order and PID, that do not provide predictive value. Both columns contain unique identifiers, which do not contribute meaningful patterns for machine learning models. Retaining such features may even degrade model performance.
To remove these columns, we use the drop method:
# Dropping irrelevant columns
df = df.drop(['Order', 'PID'], axis=1)
Here, axis=1 specifies that we are dropping columns (not rows). By reducing unnecessary data, we streamline the dataset and ensure that the model focuses on meaningful features.
4. Feature Transformation
Feature transformation involves reshaping data to improve model performance. For the Ames Housing Dataset, we identified several numerical columns with skewed distributions, which can negatively impact models like linear regression that assume normality. Applying log transformations can make these distributions closer to normal.
Identifying Skewed Features
We first calculate the skewness of all numerical columns:
# Selecting only numeric columns
numeric_cols = df.select_dtypes(include=['number'])
# Checking skewness for numeric columns
skew_vals = numeric_cols.skew()
print(skew_vals)
MS SubClass 1.356915
Lot Frontage 1.113571
Lot Area 13.154455
Overall Qual 0.171750
Overall Cond 0.573267
Year Built -0.602169
Year Remod/Add -0.448677
Mas Vnr Area 2.565828
BsmtFin SF 1 0.821599
BsmtFin SF 2 4.136716
Bsmt Unf SF 0.925413
Total Bsmt SF 0.399066
1st Flr SF 0.941362
2nd Flr SF 0.848035
Low Qual Fin SF 12.109736
Gr Liv Area 0.878650
Bsmt Full Bath 0.614609
Bsmt Half Bath 3.966772
Full Bath 0.165577
Half Bath 0.703508
Bedroom AbvGr 0.306780
Kitchen AbvGr 4.310424
TotRms AbvGrd 0.704708
Fireplaces 0.731945
Garage Yr Blt -0.381364
Garage Cars -0.220068
Garage Area 0.213447
Wood Deck SF 1.847112
Open Porch SF 2.495300
Enclosed Porch 4.011358
3Ssn Porch 11.395843
Screen Porch 3.954290
Pool Area 18.746993
Misc Val 22.228804
Mo Sold 0.196215
Yr Sold 0.132566
SalePrice 1.590763
dtype: float64
The skewness values indicate that several numeric features in the dataset have significant skewness, with notable examples being Pool Area (18.75), Misc Val (22.23), and Lot Area (13.15), which exhibit extreme right-skew. Features like Mas Vnr Area, Wood Deck SF, and Open Porch SF also have high skewness, suggesting the need for log or similar transformations. In contrast, features such as Overall Qual and Total Bsmt SF have low skewness, and some like Year Built and Year Remod/Add show mild left-skew. Addressing these skewed features will help improve data distribution and model performance.
Transforming Multiple Columns
We focus on transforming numeric features with skewness above 0.75.
skew_limit = 0.75
skewed_features = skew_vals[skew_vals > skew_limit].index
import numpy as np
# Applying log transformation to skewed features
for col in skewed_features:
df[col] = np.log1p(df[col])
This transformation effectively reduces skewness, improving data distribution for modelling. By focusing only on features with skewness above 0.75, we avoid unnecessary transformations and preserve the original scale of well-behaved features.
Verifying the Transformation
To confirm the changes, you can recheck skewness or visualize the distributions of transformed columns. For example, you can plot histograms before and after transformations to observe the improvement:
import matplotlib.pyplot as plt
# Visualizing the distribution of a transformed feature
feature = 'Lot Area' # Replace with any skewed feature
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
df_original[feature].hist()
plt.title(f'Original {feature} Distribution')
plt.subplot(1, 2, 2)
df[feature].hist()
plt.title(f'Transformed {feature} Distribution')
plt.show()
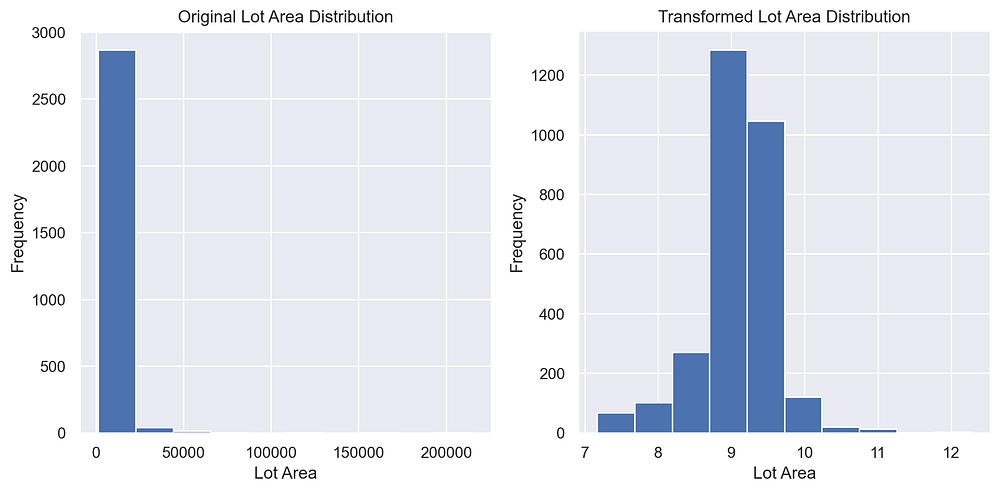
The plot shows the effect of log transformation on the Lot Area feature. The original distribution (left) is highly right-skewed, with most values concentrated near zero and a few extreme outliers. After applying the log transformation (right), the distribution becomes approximately normal, reducing skewness and making the feature more suitable for machine learning models that benefit from normally distributed inputs, such as linear regression.
5. Handling Missing Values
Missing values are a common issue in datasets and need to be addressed carefully to avoid impacting model performance. In the Ames Housing Dataset, we start by identifying missing values using isnull() and sum():
# Identifying missing values
missing_values = df.isnull().sum().sort_values(ascending=False)
print(missing_values[missing_values > 0])
Pool QC 2915
Misc Feature 2821
Alley 2728
Fence 2355
Mas Vnr Type 1774
Fireplace Qu 1422
Lot Frontage 490
Garage Cond 159
Garage Yr Blt 159
Garage Finish 159
Garage Qual 159
Garage Type 157
Bsmt Exposure 83
BsmtFin Type 2 81
BsmtFin Type 1 80
Bsmt Cond 80
Bsmt Qual 80
Mas Vnr Area 23
Bsmt Full Bath 2
Bsmt Half Bath 2
Bsmt Unf SF 1
Garage Cars 1
Electrical 1
Total Bsmt SF 1
BsmtFin SF 1 1
Garage Area 1
BsmtFin SF 2 1
dtype: int64
Replacing Missing Values for Features Indicating Absence
Some features have missing values that signify the absence of that feature in the property, not a lack of data during collection. For these features, we replace the missing values with "None":
# Replace missing values with 'None' for categorical features indicating absence
columns_to_fill_with_none = ['Pool QC', 'Misc Feature', 'Alley', 'Fence', 'Fireplace Qu']
for col in columns_to_fill_with_none:
df[col].fillna('None', inplace=True)
This ensures the absence of features like pools, fences, and fireplaces is explicitly encoded and retained for modeling.
Replacing Missing Values in Basement-Related Features
For basement-related features, missing values likely indicate the property has no basement. We handle these by replacing:
Categorical features with
"None".Numerical features with
0.
# Handling basement-related features
basement_categorical = ['Bsmt Qual', 'Bsmt Cond', 'Bsmt Exposure', 'BsmtFin Type 1', 'BsmtFin Type 2']
for col in basement_categorical:
df[col].fillna('None', inplace=True)
basement_numerical = ['BsmtFin SF 1', 'BsmtFin SF 2', 'Bsmt Unf SF', 'Total Bsmt SF', 'Bsmt Full Bath', 'Bsmt Half Bath']
for col in basement_numerical:
df[col].fillna(0, inplace=True)
This approach ensures that properties without basements are accurately represented without introducing bias.
Replacing Missing Values in Garage-Related Features
Similarly, missing values in garage-related features indicate properties without a garage. These are replaced as follows:
Categorical features are filled with
"None".Numerical features are filled with
0.
# Handling garage-related features
garage_categorical = ['Garage Type', 'Garage Finish', 'Garage Qual', 'Garage Cond']
for col in garage_categorical:
df[col].fillna('None', inplace=True)
garage_numerical = ['Garage Yr Blt', 'Garage Area', 'Garage Cars']
for col in garage_numerical:
df[col].fillna(0, inplace=True)
Replacing Missing Values in Other Features
Features like Lot Frontage and Mas Vnr Area require imputation based on the dataset’s context:
Lot Frontage: Missing values are imputed with the median, as it balances the influence of outliers.Mas Vnr AreaandMas Vnr Type: Missing values are replaced with0and"None", respectively.
# Filling remaining features
df['Lot Frontage'].fillna(df['Lot Frontage'].median(), inplace=True)
df['Mas Vnr Area'].fillna(0, inplace=True)
df['Mas Vnr Type'].fillna('None', inplace=True)
Replacing Minimal Missing Values
For features with very few missing values, we impute reasonable defaults:
Electrical: Replaced with the mode (most common value).Other minimal missing numerical features: Replaced with
0.
# Filling minimal missing values
df['Electrical'].fillna(df['Electrical'].mode()[0], inplace=True)
Verifying All Missing Values Are Handled
Finally, we ensure that no missing values remain in the dataset:
# Check for remaining missing values
print(df.isnull().sum().max()) # Should return 0
0
By addressing missing values based on their context, we retain critical information while ensuring the dataset is clean and complete. This thoughtful approach enhances data quality and prepares the dataset for further preprocessing and modeling.
6. Creating New Features
Creating new features can significantly improve model performance by capturing non-linear relationships, interactions, and relative deviations within the data. In the Ames Housing Dataset, we explore three key techniques: polynomial features, interaction terms, and relative deviations.
Polynomial Features
Polynomial features allow us to model non-linear relationships by expanding numerical features into higher-order terms and their interactions. For example, squaring a feature or including its interaction with another feature can provide the model with more expressive input data.
Here’s how we generate polynomial features using Scikit-learn’s PolynomialFeatures:
from sklearn.preprocessing import PolynomialFeatures
# Select numerical columns for polynomial transformation
numerical_cols = ['Lot Area', 'Overall Qual'] # Example numerical columns
# Create polynomial features
poly = PolynomialFeatures(degree=2, include_bias=False)
poly_features = poly.fit_transform(df[numerical_cols])
# Convert to a DataFrame
poly_feature_names = poly.get_feature_names_out(numerical_cols)
poly_df = pd.DataFrame(poly_features, columns=poly_feature_names)
# Add polynomial features to the dataset
df = pd.concat([df, poly_df], axis=1)
Visualizing Polynomial Expansion
If Lot Area and Overall Qual are the input features, the polynomial expansion includes:
Lot Area(original feature),Overall Qual(original feature),Lot Area²(squared term),Lot Area × Overall Qual(interaction term),Overall Qual²(squared term).
This expansion transforms two features into five, providing the model with richer information to capture non-linear patterns.
Interaction Features
Interaction terms capture the combined effect of two features. For example, the interaction between Overall Qual and Year Built can represent the compounded impact of quality and property age on the target variable.
Here’s how we create interaction terms manually:
# Creating interaction features
df['OverallQual_YearBuilt'] = df['Overall Qual'] * df['Year Built']
df['QualPerLotArea'] = df['Overall Qual'] / df['Lot Area']
These features encode relationships between variables that the model might otherwise struggle to learn.
Relative Deviations
Relative deviations provide context by comparing a feature’s value to the average within its category. For example, we calculate how much a house’s Overall Qual deviates from the average Overall Qual in its neighborhood.
Using groupby().transform(), we calculate deviations as follows:
# Calculate mean and standard deviation of Overall Qual within each Neighborhood
neighborhood_stats = df.groupby('Neighborhood')['Overall Qual'].agg(
mean_neigh='mean',
std_neigh='std'
).reset_index()
# Merge the stats back into the original dataset
df = df.merge(neighborhood_stats, on='Neighborhood', how='left')
# Calculate the deviation of Overall Qual within each neighborhood
df['Qual_Deviation'] = (df['Overall Qual'] - df['mean_neigh']) / df['std_neigh']
This feature provides insight into whether a house is above or below average quality for its neighborhood, offering valuable context for models.
By generating polynomial features, creating interaction terms, and calculating relative deviations, we enrich the dataset with meaningful information, enabling models to better capture complex relationships in the data. These feature engineering techniques are instrumental in improving predictive performance.
7. Handling Categorical Data
Handling categorical data involves transforming non-numeric features into a format that machine learning models can process effectively. In the Ames Housing Dataset, we reduce the dimensionality of categorical features before applying encoding techniques to ensure a clean and efficient dataset.
Reducing Dimensionality in Categorical Features
Reducing dimensionality in categorical features is crucial for simplifying the dataset and avoiding sparsity when applying one-hot encoding. In the Ames Housing Dataset, the Neighborhood and House Style features have several unique categories, including some with very low frequencies. To address this, we group low-frequency categories into an "Other" category before applying encoding.
The Neighborhood variable contains 25 unique values, representing different areas of the city. Here is a sample of their counts:
df['Neighborhood'].value_counts()
Neighborhood
NAmes 444
CollgCr 267
OldTown 239
Edwards 191
Somerst 182
NridgHt 166
Gilbert 165
Sawyer 151
NWAmes 131
SawyerW 125
Mitchel 114
BrkSide 108
Crawfor 103
IDOTRR 93
Timber 72
NoRidge 69
StoneBr 51
SWISU 48
ClearCr 44
MeadowV 37
BrDale 30
Blmngtn 28
Veenker 24
NPkVill 23
Blueste 10
Greens 8
GrnHill 2
Landmrk 1
Name: count, dtype: int64
Some categories, such as Landmrk (1 occurrence) and GrnHill (2 occurrences), are extremely rare. Including these as separate one-hot encoded columns would add unnecessary complexity and sparsity. To address this, we group categories with fewer than 10 occurrences into an "Other" category:
# Group low-frequency neighborhoods into "Other"
low_count_neighborhoods = df['Neighborhood'].value_counts()[df['Neighborhood'].value_counts() < 10].index
df['Neighborhood'] = df['Neighborhood'].replace(low_count_neighborhoods, 'Other')
The House Style variable contains 8 unique values, each representing a different architectural style. Their frequencies are as follows:
df['House Style'].value_counts()
House Style
1Story 1481
2Story 869
1.5Fin 314
SLvl 128
SFoyer 83
2.5Unf 24
1.5Unf 19
2.5Fin 8
Name: count, dtype: int64
Categories like 2.5Fin (8 occurrences) and 1.5Unf (19 occurrences) are rare and can add noise when one-hot encoded. To simplify the dataset, we group categories with fewer than 50 occurrences into an "Other" category:
# Group low-frequency house styles into "Other"
low_count_styles = df['House Style'].value_counts()[df['House Style'].value_counts() < 50].index
df['House Style'] = df['House Style'].replace(low_count_styles, 'Other')
After this transformation, the unique values in House Style are reduced to:
1Story2Story1.5FinSLvlSFoyerOther
One-Hot Encoding
After reducing dimensionality, we apply one-hot encoding to transform categorical features into binary columns. For example, the Neighborhood feature is converted into multiple binary columns representing each category while avoiding multicollinearity by dropping the first category:
# Apply one-hot encoding to categorical features
df = pd.get_dummies(df, columns=['Neighborhood', 'House Style'], drop_first=True)
columns: Specifies the categorical features to encode.drop_first=True: Removes one category per feature to avoid multicollinearity in linear models.
Encoding Ordinal Features
Some categorical features, like Exter Qual (Exterior Quality), have an intrinsic order (e.g., Poor < Fair < Good < Excellent). For these features, ordinal encoding is applied to preserve their order:
# Ordinal encoding for Exter Qual
exter_qual_map = {'Poor': 1, 'Fair': 2, 'Good': 3, 'Excellent': 4}
df['Exter Qual'] = df['Exter Qual'].map(exter_qual_map)
This replaces the categories with their corresponding numerical values, maintaining the ordinal relationship.
8. Correlation Analysis
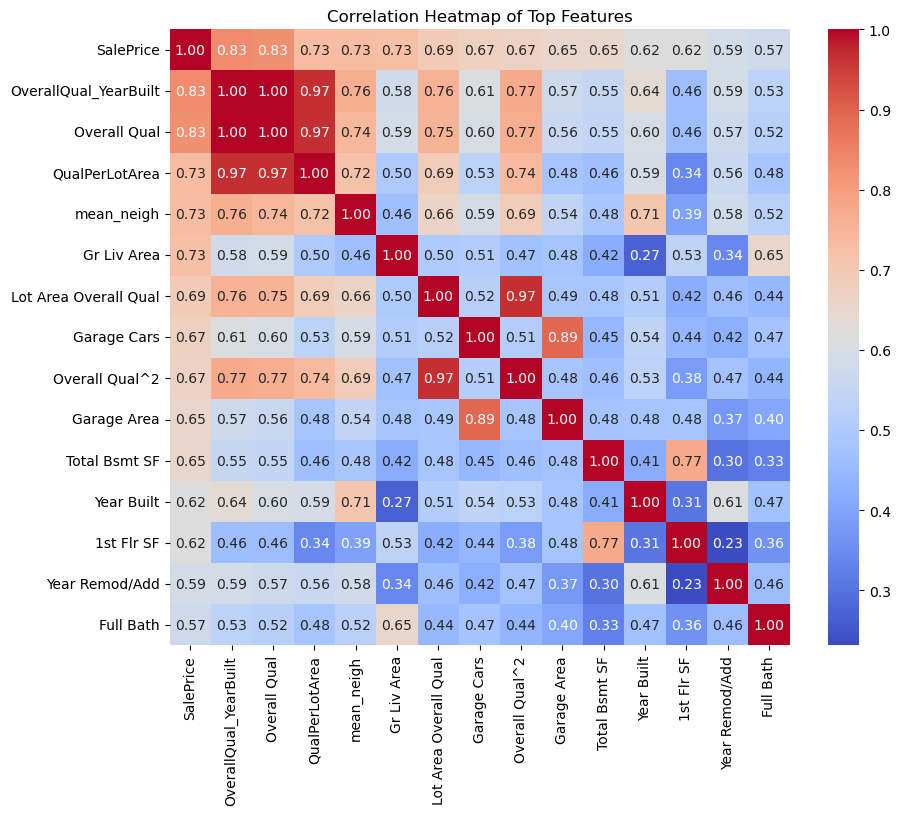
Given the large number of features in the dataset, a full heatmap may be overwhelming and difficult to interpret. Instead, we focus on identifying features most strongly correlated with the target variable, SalePrice, using a sorted list of correlation values. This approach simplifies the analysis and highlights the most relevant features.
Correlation with SalePrice
We extract and sort the correlation values of all features with SalePrice to identify the strongest relationships:
# Calculate the correlation matrix
correlation_matrix = df.corr(numeric_only=True)
# Extract and sort correlations with SalePrice
target_corr = correlation_matrix['SalePrice'].sort_values(ascending=False)
print(target_corr)
SalePrice 1.000000
OverallQual_YearBuilt 0.834162
Overall Qual 0.827489
QualPerLotArea 0.733817
mean_neigh 0.730479
...
Neighborhood_Edwards -0.194731
Enclosed Porch -0.220051
Neighborhood_IDOTRR -0.243680
Neighborhood_OldTown -0.255239
Exter Qual NaN
Name: SalePrice, Length: 76, dtype: float64
Selecting the Top Correlated Features
Based on the sorted correlations, we select the top features with high absolute correlation values (e.g., above 0.5):
# Select top correlated features with SalePrice
top_features = target_corr[target_corr.abs() > 0.5]
print("Top features correlated with SalePrice:")
print(top_features)
Top features correlated with SalePrice:
SalePrice 1.000000
OverallQual_YearBuilt 0.834162
Overall Qual 0.827489
QualPerLotArea 0.733817
mean_neigh 0.730479
Gr Liv Area 0.726131
Lot Area Overall Qual 0.692244
Garage Cars 0.674913
Overall Qual^2 0.668838
Garage Area 0.653704
Total Bsmt SF 0.649027
Year Built 0.616685
1st Flr SF 0.616530
Year Remod/Add 0.587420
Full Bath 0.574949
Name: SalePrice, dtype: float64
This gives a concise list of features most strongly associated with SalePrice.
Analyze Relationships Between Features
To evaluate the relationships between features (including multicollinearity), we can create a heatmap of the correlation matrix for the top features:
# Calculate the correlation matrix for top features
correlation_matrix = df[top_corr_features].corr()
# Plot the heatmap
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, fmt=".2f", cmap="coolwarm", cbar=True)
plt.title("Correlation Heatmap of Top Features")
plt.show()
This heatmap highlights the correlations between the top features and SalePrice, as well as between the features themselves. Key observations include:
Strong Correlation with
SalePrice: Features likeOverall Qual,Gr Liv Area,OverallQual_YearBuilt, andGarage Carsshow strong positive correlations withSalePrice(above 0.7), indicating their importance for predicting house prices.Multicollinearity:
Garage CarsandGarage Areaare highly correlated (0.89), suggesting redundancy. Retaining both could lead to multicollinearity issues.Overall Qualand its engineered features (OverallQual_YearBuilt,Overall Qual^2) are also highly correlated, reflecting overlapping information.
3. Moderate Correlation: Features like Year Built and Year Remod/Add exhibit moderate correlations with SalePrice (~0.6) and overlap to some extent.
This analysis suggests focusing on highly correlated features while addressing multicollinearity through regularization or feature reduction.
Pair Plot for Top Features
To visualize the relationships between the top correlated features and SalePrice, we use a pair plot:
# Extract the list of top correlated features
top_corr_features = top_features.index.tolist()
# Define the maximum number of subplots per row
max_subplots_per_row = 5
# Exclude SalePrice itself
features = top_corr_features[:-1]
# Split features into groups of 5
feature_groups = [features[i:i + max_subplots_per_row] for i in range(0, len(features), max_subplots_per_row)]
# Plot each group in separate rows
for group_idx, feature_group in enumerate(feature_groups):
plt.figure(figsize=(20, 4)) # Adjust figure size based on the number of subplots
for i, feature in enumerate(feature_group):
plt.subplot(1, len(feature_group), i + 1)
sns.scatterplot(data=df, x=feature, y='SalePrice', alpha=0.1, edgecolor='none')
plt.title(feature)
plt.suptitle(f"Pair Plot of Top Features with SalePrice (Row {group_idx + 1})", y=1.02)
plt.tight_layout()
plt.show()
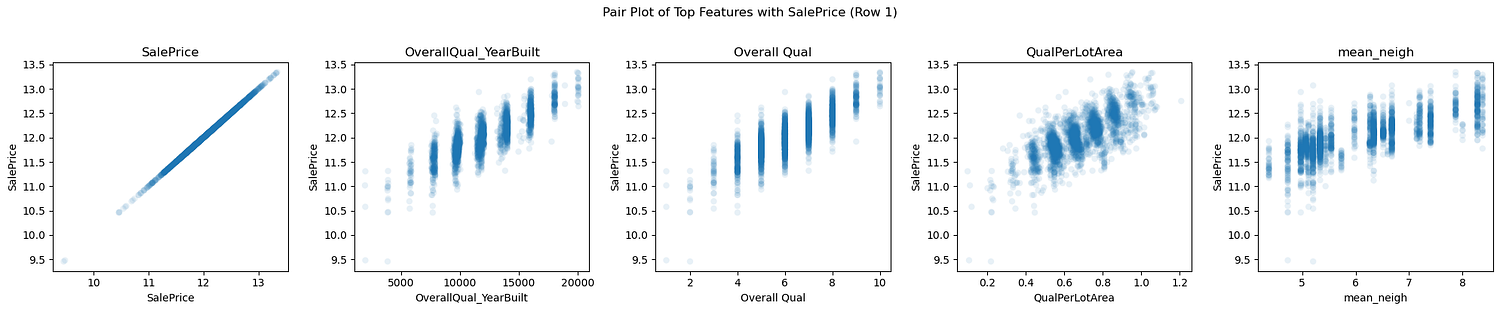
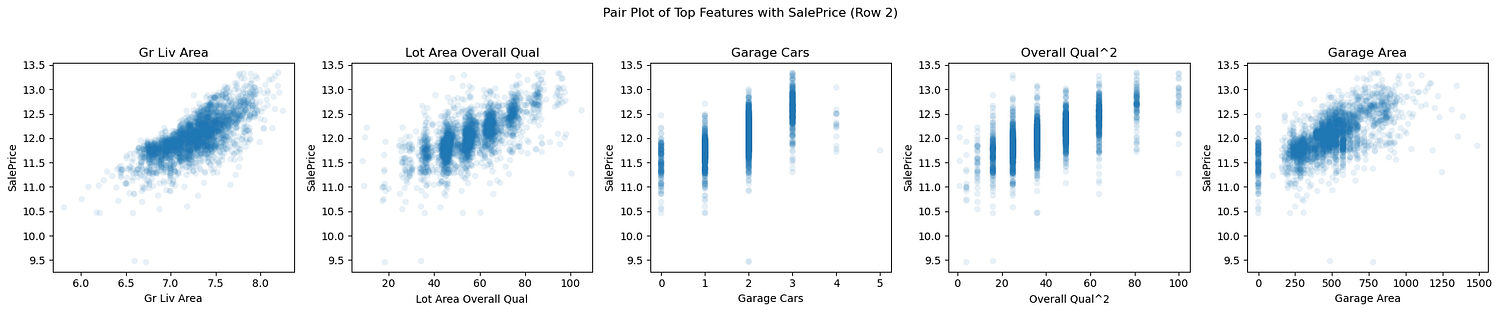
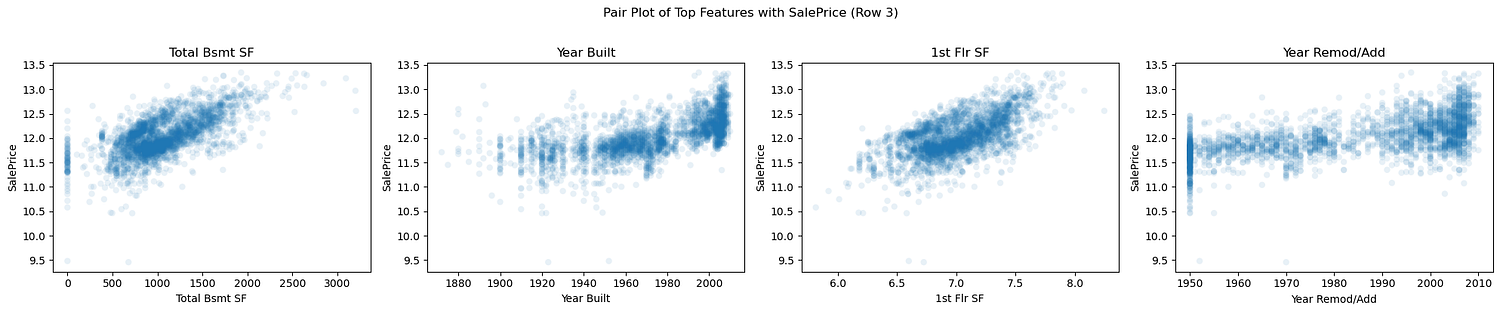
1. What do these plots tell us about the distribution of the target?
The target variable, SalePrice, appears to have a right-skewed distribution across some features, such as Year Built and Garage Area, where most data points are clustered at lower SalePrice values. However, features like Overall Qual and Gr Liv Area exhibit a broader and more even spread of SalePrice, indicating strong linear relationships across the range. This mixed behavior suggests that while linear regression may be effective, the skewness in specific features could still introduce biases in model residuals, making a log transformation of SalePrice or those specific features is a useful step.
2. What do these plots tell us about the relationship between the features and the target? Do you think that linear regression is well-suited to this problem? Do any feature transformations come to mind?
Most features, such as Overall Qual, Gr Liv Area, and QualPerLotArea, exhibit positive linear relationships with SalePrice. These relationships suggest that linear regression is well-suited to model these features. However, some features, such as Year Built and Year Remod/Add, exhibit more subtle trends, with some noise at higher SalePrice values. For these, interaction terms (e.g., OverallQual_YearBuilt) or polynomial features (e.g., Overall Qual^2) could improve model fit. The log transformation already applied to some features (e.g., Lot Area) effectively normalizes skewed relationships, aligning them better with SalePrice.
9. Conclusion
In this blog, we explored the Ames Housing dataset, focusing on feature engineering and its importance in preparing data for predictive modeling. We performed extensive Exploratory Data Analysis (EDA), handled missing values, applied transformations to address skewness, engineered new features, and analyzed correlations to understand relationships between variables. These steps ensured the dataset was ready for building robust machine learning models. The insights gained, such as identifying critical features (Overall Qual, Gr Liv Area, etc.) and handling multicollinearity, provide a strong foundation for accurate predictions.
10. Next Steps
The next steps involve leveraging the preprocessed and feature-engineered dataset to train machine learning models. Key actions include:
Splitting the dataset into training and testing sets.
Applying machine learning algorithms, starting with linear regression, to assess the model’s performance.
Exploring advanced techniques like Ridge, Lasso, or Gradient Boosting to address multicollinearity and improve predictive accuracy.
Validating the model using cross-validation techniques.
Deploying the final model for real-world applications, such as house price prediction.